Уравнивание полигонометрического хода параметрическим способом

При обработке полигонометрии на ЭВМ целесообразно применение параметрического способа уравнивания. В этом случае составляются параметрические уравнения поправок для всех измеренных углов и длин линий (рис. 19.1):

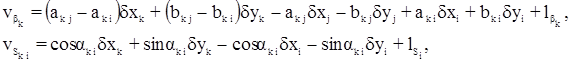
где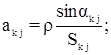

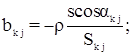
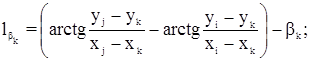
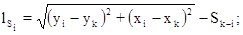
где х, у – приближенные координаты пунктов;

β – измеренные значения углов;

S – измеренное значение линии.

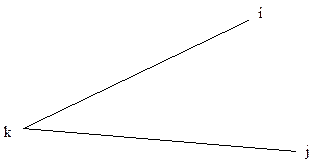
Рисунок 19.1 – Схема измеренного угла

Решая систему (n_β + n_S) параметрических уравнений поправок при условии 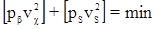приходим к 2n нормальных уравнений (п – число определяемых пунктов):

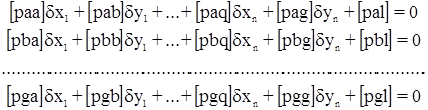
Веса вычисляются по формулам:

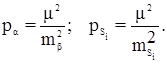
Вычислив поправки к приближенным координатам пунктов dx и dy, находим их уравненные значения:

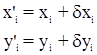
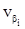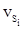По параметрическим уравнениям поправок вычисляются поправки в измеренные элементы и , а затем их уравненные значения:

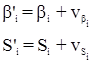
Оценка точности выполняется по формулам:

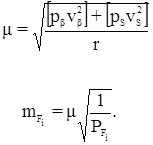
УРАВНИВАНИЕ ПОЛИГОНОМЕТРИЧЕСКИХ СЕТЕЙ

Общие положения

Уравнение сетей полигонометрии при условии [pv²] = min выполняется параметрическим или коррелатным способами, двухгрупповым коррелатным или коррелатным способ с дополнительными неизвестными.

При нестрогой обработке полигонометрических сетей применяются раздельные способы уравнивания, когда сначала уравниваются углы, а затем раздельно между собой - приращения координат. Раздельное уравнение выполняется способами:

- эквивалентной замены ;

- узлов профессора Попова В.В. (с решении методом последовательных приближений или с составлением и решением системы нормальных уравнений узлов);

- полигонов профессора Попова В.В.

Выбор способа уравнения зависит от:

- строгости требований;

- величины сети;

- наличия исходных пунктов;

- конфигурации сети;

- наличия ЭВМ;

- экономических соображений.

Строгое уравнивание больших полигонометрических сетей производят на ЭВМ, коррелатным способом с дополнительными неизвестными, или параметрическим способом.