Уравнивание полигонометрической сети двухгрупповым коррелатным способом

При наличии исходных дирекционных углов на узловых пунктах, а также при измерении по два примычных угла в исходных пунктах целесообразно применение двухгруппового способа уравнивания. В этом случае вводятся центральные координаты , соединяющего для каждого хода сети, соединяющего узловые пункты с исходными (рис. 20.3). например, в данной сети измерено 16 углов и 9 линий для определения положения 7 новых пунктов полигонометрии, т.е. число избыточных измерений составляет:

R = (16 + 9) – (7·2) = 11,

В том числе:

r_α = N + T + Q – 1 = 0 + 3 + 1 – 1 = 3,

r_X,Y = (N + T – 1)·2 = (0 + 3 – 1)·2 = 4,

r_гор = 1,

r_угл = 3.

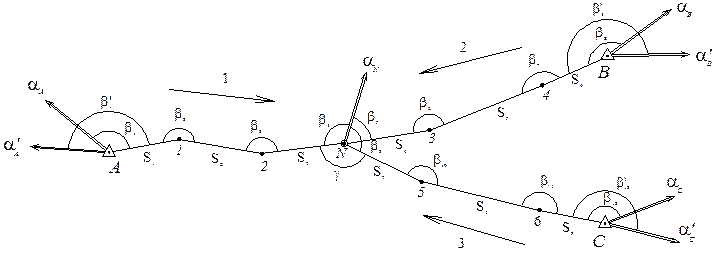
Рисунок 20.3 – Схема сети

При этом в 7 уравнениях дирекционных углов, примычных углов и горизонта все коэффициенты равны ±1. Эти уравнения включаются в 1-ю группу и решаются совместно. А затем решаются 4 преобразованные условные уравнения координат.

Рассмотрим вид этих условных уравнений поправок:

I – угловые:

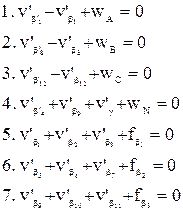
II – координатные:

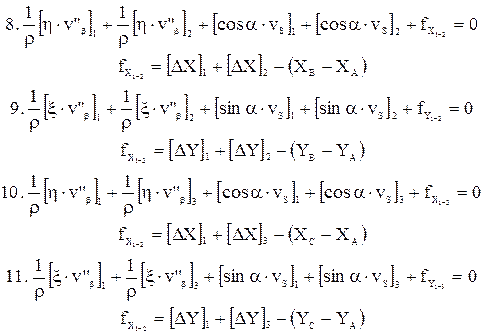
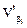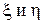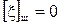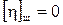Невязки f_X и f_Y вычислены после предварительного исправления углов введением первичных поправок ; - центральные координаты для каждого хода, т.е. и . Если в полигонометрической сети возникают только уравнения 5-11 (т.е. нет условия горизонта и углов) , то каждое из угловых уравнений (5, 6, 7) решается отдельно, а затем совместно решаются четыре условных уравнения координат (8-11). В остальном ход уравнивания и оценки точности не отличается от уравнивания одиночного хода.