Раздельное (приближенное) уравнивание полигонометрической сети с одной узловой точкой

При раздельном уравнивании сначала уравнивают углы сети, а затем по уравненным углам и измеренным длинам линий вычисляют приращения координат и уравнивают отдельно приращения абсцисс и приращения ординат. При уравнивании углов сначала выбирают условное узловое направление, которое разделит всю сеть на отдельные ходы (рис. 20.4). дирекционный угол узлового направления α_N = a_NM можно вычислить по ходам от каждого исходного направления.

Рисунок 20.4 – Схема сети

Веса этих значений дирекционного угла узлового направления можно вычислить по формуле:

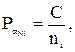
где n – количество углов в каждом ходе.

Уравненное значение дирекционного угла узлового направления определяют по формуле:

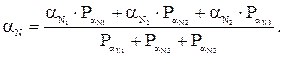
По невязкам 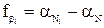исправляют углы в каждом отдельном ходе на поправку :

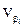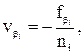
т.е. поровну во все углы хода. Затем по уравненным углам вычисляют дирекционные углы и приращения координат. По каждому ходу вычисляют координаты узловой точки:

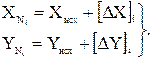
Веса найденных координат узловой точки можно вычислить по формулам:

,

или

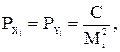
или

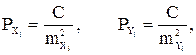
где 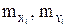- средние квадратические погрешности определения координат конечной точки хода;

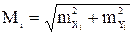- средняя квадратическая погрешность определения положения конечной точки хода;

[S]_i – длина i-того хода.

Т.к. раздельное уравнивание является приближенным, обычно веса устанавливают по первой из формул. Уравненное значение координат узловой точки вычисляют по формулам:

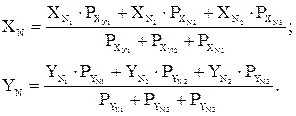
Невязки в приращения координат

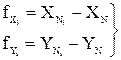
распределяют пропорционально длинам линий по каждому ходу отдельно. Для оценки точности применяют формулы:

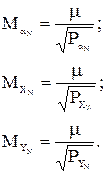
где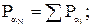

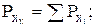
Средняя квадратическая погрешность единицы веса определяется по формуле:

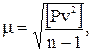
где P и v – веса и поправки дирекционных углов или координат;

n – число ходов.