Уравнивание полигонометрической сети коррелатным способом

Число условий, возникающих в сети, определяется по формуле:

R = (N + T – 1)·3,

где N – число замкнутых полигонов;

Т – число исходных пунктов в сети.

Если на узловых пунктах были измерены (определены по астрономическим или гироскопическим наблюдениям) дирекционные углы, то:

R = (N +T – 1)·3 + Q,

где Q – количество измеренных дирекционных углов в узловых пунктах.

Из всех условий будем иметь r_α условий дирекционных углов и r_X,Y условий координат. Кроме того, в сети могут возникать условия горизонта и твердого угла. Для составления условных уравнений поправок по схеме сети намечают замкнутые и разомкнутые полигоны, опирающиеся на исходные пункты. При этом все полигоны должны быть независимыми и все ходы должны быть включены в полигоны. Намеченные полигоны нумеруют, а их направление показывают стрелкой (рис.20.1).

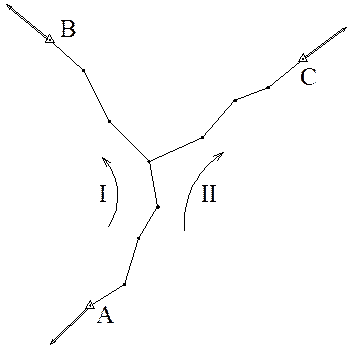
Рисунок 20.1 – Схема полигонометрической сети

r = (0 + 3 – 1)·3 = 6,

r_α = 0 + 3 – 1 = 2,

r_X,Y = 2·(0 + 3 – 1) = 4,

т.е. в такой системе 6 условных уравнений, из которых 2 – дирекционных углов и 4 – координат.

Эти уравнения имеют вид:

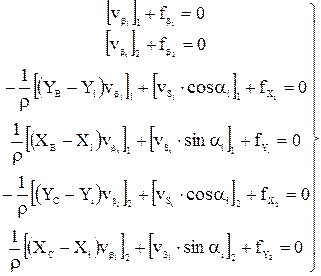
Если в сети измерялись по два примычных угла в исходных пунктах (рис. 20.2), то условные уравнения поправок угла имеют вид:

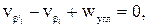
где w_угл = b’₁ – b₁ – (a_T’ – a_T).

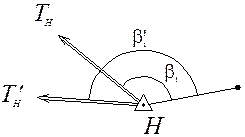
Рисунок 20.2 – Схема примыкания к двум пунктам

Эти условия необходимо составлять не только для контроля, но и включать их в уравнивание, т.к. это повышает вес уравненных элементов сети. Аналогично поступают с условием горизонта, когда в узловом пункте измерены не только необходимые углы, но и углы, замыкающие горизонт.

От условных уравнений в соответствии с принципом наименьших квадратов переходят к системе нормальных уравнений коррелат, число которых равно числу условий. По найденным из решения нормальных уравнений коррелатам определяют поправки в углы и длины линий. Дальнейший процесс уравнивания и оценки точности полигонометрической сети такой же, как и при уравнивании отдельного полигонометрического хода.