Уравнивание коррелатным способом хода, опирающегося на исходные пункты и направления

Рассмотрим схему хода (рис. 19.1). В таком ходе общее измерение составляет п – линий и п + 1 углов, т.е. всего (2п + 1) измерений. Количество необходимых измерений составляет 2(п – 1). следовательно, число избыточных измерений r = (2n + 1) - 2(п – 1) = 3.

Рисунок 19.1 – Схема полигонометрического хода

Возникают три условных уравнения поправок:

дирекционных углов;

абсцисс;

ординат.

Эти уравнения имеют вид:

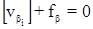
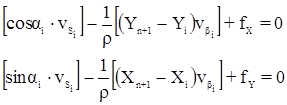
где 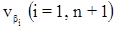– поправки в измеренные углы;

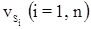– поправки в измеренные длины линий;

X_i, Y_i (i = Нач, 1,2, …, n-1, Кон) – координаты текущей точки хода, в которой измерен угол b_i;

X_n, Y_n – координаты конечной точки хода.

При этом a_i, f_X, f_Y вычисляются без предварительного распределения угловой невязки. Для упрощения вычислений координаты пунктов полигонометрии могут вычисляться в условной системе, когда координаты начального пункта приравниваются к нулю.

Система нормальных уравнений коррелат имеет вид:

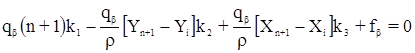
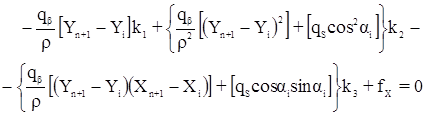
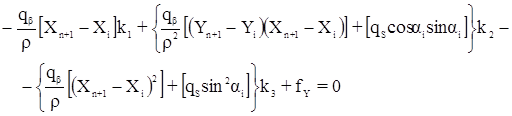
Здесь 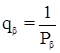- обратный вес измеренных углов, 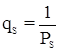- обратные веса измеренных длин линий. В результате решения нормальных уравнений определяют коррелаты k₁, k₂ и k₃. Поправки в измеренные углы вычисляются по формуле:

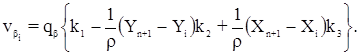
Контроль: .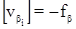

Поправки в измеренные длины линий вычисляются по формуле:

.

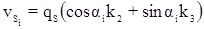Поправки в предварительные значения дирекционных углов вычисляются по формуле:

.

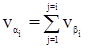Уравненные углы, дирекционные углы и длины линий находят введением поправок v_b, v_a и v_S в значения b, a и S. Уравненные значения приращений координат вычисляют по уравненным дирекционным углам и длинам линий:

.

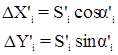Контроль:[DX’_i] = X_к – Х_н; [DY’_i] = Y_к – Y_н.

Кроме того, поправки в приращения координат можно вычислить по формуле:

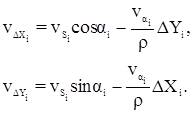
Контроль: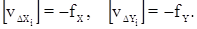

В этом случае уравненные приращения координат вычисляются по формулам:

.

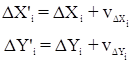Уравненные координаты пунктов полигонометрического хода вычисляются по формулам: