Обратная однократная засечка
Определение положения точки по трем исходным пунктам обратной угловой засечкой называется задачей Потенота. Существует несколько способов решения этой задачи.
17.7.1 Формула Деламбра используется для вычисления дирекционного угла линии Р-Т1 (рис. 17.6):
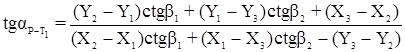 .
.
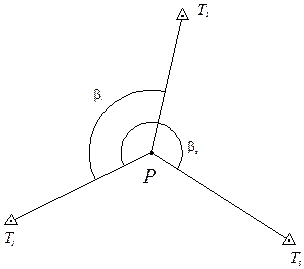
Рисунок 17.6 – Схема обратной однократной засечки
Далее вычисляют дирекционные углы:
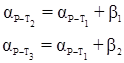 .
.
Координаты определяемой точки вычисляются по формулам Гаусса:
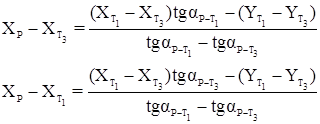 ,
,
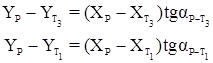 .
.
Заключительный контроль:
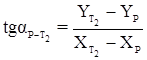 .
.
Полученное по этой формуле значение дирекционного угла 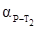 является окончательным. Оно может отличаться от найденного по формуле Деламбра на 1800, т.к. в ней знаки числителя и знаменателя не определяют знаки
является окончательным. Оно может отличаться от найденного по формуле Деламбра на 1800, т.к. в ней знаки числителя и знаменателя не определяют знаки 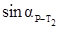 и
и 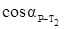 . В этом случае
. В этом случае 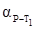 и
и 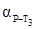 также должны быть изменены на 1800.
также должны быть изменены на 1800.
17.7.2 Формулы И. Ю. Пранис-Праневича

Рисунок 17.7 – Схема наблюдений
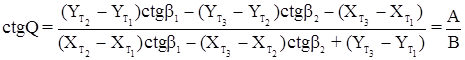 .
.
Затем вычисляют с контролем величину N:
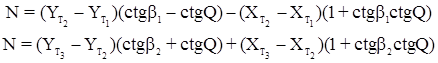 .
.
Координаты вычисляют по формулам:
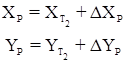 ,
,
где 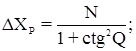
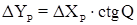 .
.
Поскольку контроль вычисления координат точки Р отсутствует, то требуются наблюдения на 4-й исходный пункт.
17.7.3 Обобщенные формулы
Возможны два варианта обратной угловой засечки определяемого пункта:
по двум несмежным углам (рис. 17.8 а);
· по двум смежным углам (рис. 17.8 б).

а б
Рисунок 17.8 – Варианты обратной угловой засечки
Общее решение сводится к отысканию точек пересечения двух окружностей, вмещающих измеренные углы b1 и b2 (рис. 17.8 а), радиусы и координаты центров окружностей вычисляются по формулам:
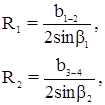
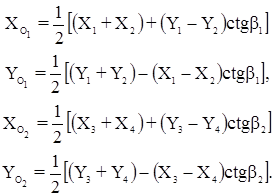
В треугольнике О1О2Р находим:
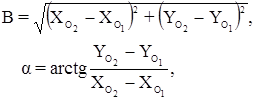
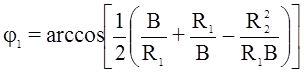 ,
,
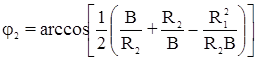 .
.
Далее находим направления:
aI = a ± j1,
aII= a ± 1800 ± j2
и координаты:
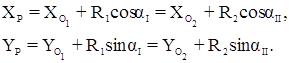
Для разрешения неопределенности в выборе точки стояния целесообразно дополнительно измерить магнитный азимут на один из исходных пунктов. Это решение справедливо и для задачи Потенота, если принять, что исходные пункты 2 и 3 совпадают (рис. 17.8 б).
17.7.4 Точность обратной засечки
Средняя квадратическая погрешность определения положения искомого пункта вычисляется по формулам:
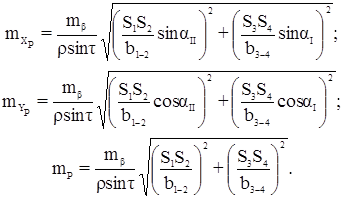
Дата добавления: 2016-06-02; просмотров: 3708;
