Вес функции независимых величин

Определим вес функции

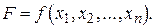(2.27)

При этом известны веса аргументов p₁ , p₂ , . . . , p_n. В случае независимых величин имеем

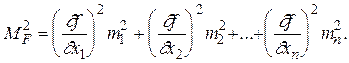(2.28)

Разделим обе части равенства (2.28) на m²

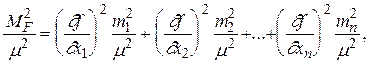
так как 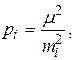то окончательно имеем

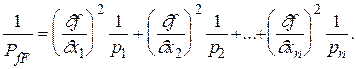(2.29)

Вес функции неравноточных слагаемых

Дана функция вида

F = x₁ + x₂ + . . . + x_n , (2.30)

где x_i - результаты неравноточных измерений с соответствующими весами: p₁, p₂ , . . . , p_{n .}

Требуется определить вес функции F . Cогласно (2.29) будем иметь

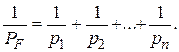(2.31)

Обратный вес суммы неравноточных слагаемых равен сумме обратных весов.

Вес суммы равноточных слагаемых

Дана функция вида (2.30), в которой x_i являются результатами равноточных измерений, т.е. p₁ = p₂ = . . . = p_n = p. Тогда вес такой функции определится из равенства (2.31)

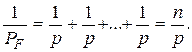(2.32)

Откуда

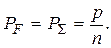(2.33)

Вес суммы равноточных слагаемых в n раз меньше веса одного измерения.

Вес простой арифметической средины

Поскольку простая арифметическая средина вычисляется согласно формуле

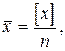(2.34)

ее средняя квадратическая ошибка будет равна

,

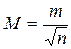откуда

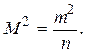
Переходя к весам, получим

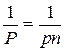
или

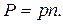(2.35)

Вес простой арифметической средины в n раз больше веса одного измерения.

Вес и средняя квадратическая ошибка