Общая арифметическая средина и ее свойства

Пусть дан ряд результатов измерений

x₁ , x₂ , . . . , x_n ;

m₁ , m₂ , . . . , m_n .

Требуется найти наиболее надежное значение`x измеренной величины. Выразим искомую величину в виде линейной функции

(2.2)

где k_i являются некоторой функцией величин m_i и связаны условием

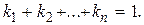(2.3)

Тогда

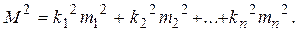(2.4)

Функция приведет нас к надежному результату, если ее средняя квадратическая ошибка будет наименьшей, т. е.

M² = min . (2.5)

Задачу решим по методу Лагранжа

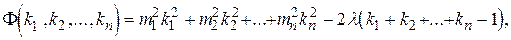(2.6)

где l - подлежащий определению коэффициент, называемый множителем Лагранжа.

Условие (2.5) определяется точкой экстремума функции Лагранжа F.

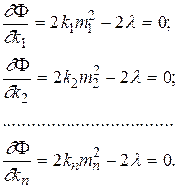(2.7)

Отсюда

(2.8)

Подставив эти значения в уравнение (2.2), получим

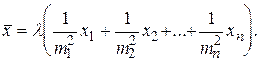(2.9)

Из уравнения (2.8) найдем

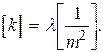(2.10)

С учетом равенства (2.3) определим множитель Лагранжа l

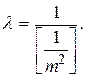(2.11)

Полученное значение l подставим в уравнение (2.9)

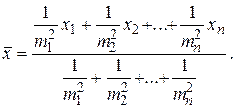(2.12)

Учитывая (2.1), равенство (2.12) можно записать в следующем виде:

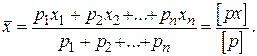(2.13)

Общая арифметическая средина равна сумме произведений каждого неравноточного измерения на его вес, разделенной на сумму весов.

Рассмотрим свойства отклонений от общей арифметической средины.
Первое свойство. Алгебраическая сумма произведений отклонений результатов неравноточных измерений от общей арифметической средины на соответствующие веса равна нулю при любом числе наблюдений, т.е.

[ pv ] = 0 . (2.14)

Дан ряд отклонений от арифметической средины с соответствующими весами p_{1 ,} p_{2 , . . . ,} p_n.
p₁ v₁ = x₁ - `x ;
p<sub>2</sub> v<sub>2</sub> = x<sub>2</sub> - `x ;
. . . . . . . . . . . . (2.15)

p_n v_n = x_n - `x .

Перемножив равенства (2.15) на соответствующие веса и сложив левую и правую части, получим

Cогласно (2.13) будем иметь

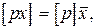
следовательно,

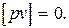(2.16)

Данное свойство можно использовать для контроля вычислений общей арифметической средины.

Второе свойство. Cумма произведений квадратов отклонений результатов неравноточных измерений от общей арифметической средины на соответствующие веса является наименьшей, т.е

[ pvv ] = min (2.17)

Пусть x¢ ¹ `x , тогда

(2.18)

Установим связь между отклонениями v и v¢

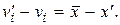(2.19)

В равенстве (2.19) v_i перенесем в правую часть. Затем, умножая на соответствующие веса, возведем в квадрат и почленно сложим

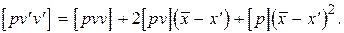(2.20)

В правой части равенства (2.20) слагаемое 2 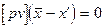согласно первому свойству отклонений (2.16). Следовательно, из равенства (2.20) следует, что

(2.21)

Данное свойство подтверждает, что если ошибки результатов неравноточных измерений подчиняются нормальному закону распределения, то наиболее надежным значением является общая арифметическая средина.

2.3. Средняя квадратическая ошибка единицы веса

Дан ряд результатов неравноточных измерений

x₁ , x₂ , . . . , x_n ;

m₁ , m₂ , . . . , m_n .

Cоответственно

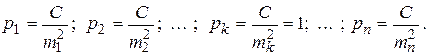(2.22)

Как видим из равенств (2.22) , всегда найдется такое соотношение, когда 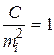, т.е. коэффициент С есть не что иное, как средняя квадратическая ошибка измерения, вес которой равен единице и которая в отличие от остальных средних квадратических ошибок обозначается m и называется ошибкой единицы веса.

Тогда

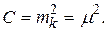(2.23)

Следовательно,

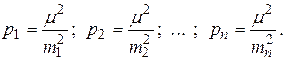(2.24)

В соответствии с (2.24) можно записать

(2.25)

или
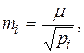(2.26)

т.е. cредняя квадратическая ошибка любого результата измерения равна ошибке единицы веса, деленной на корень квадратный из веса соответствующего результата.

2.4. Вычисление весов функций