Раздел III ТРИЛАТЕРАЦИЯ
10 ПОСТРОЕНИЕ И УРАВНИВАНИЕ ТРИЛАТЕРАЦИИ
10.1 Общие сведения о трилатерации
При основных геодезических работах должен быть обоснован оптимальный выбор метода и схема построения или сгущения государственной геодезической сети.
Метод полигонометрии целесообразно применять на тех объектах, где применение триангуляции требует сплошной постройки высоких знаков. Метод трилатерации особенно эффективен в случае применения радиодальномеров с отделенными приемопередатчиками и переносных мачт.
Трилатерация – метод построения геодезической сети в виде треугольников, в которых измерены все их стороны. При развитии и сгущении ГГС 3 и 4 классов методом трилатерации схема сети (длины сторон, наименьшие и наибольшие углы треугольников) должна быть такой же, как и в триангуляции соответствующего класса. Стороны сети трилатерации должны быть измерены с относительными средними квадратическими погрешностями mS/S = 1:100 000 (3 класс) и mS/S = 1:40 000 (4 класс).
Принципиальные схемы сгущения сети показаны на рисунке.
Если при проектировании сетей сгущения 3-4 классов расстояние между двумя любыми пунктами оказывается меньше 3 км, то необходимо предусматривать непосредственное его измерение. При связи сети трилатерации с ранее исполненными сетями должны быть повторно измерены все стороны вдоль границы.
На каждом пункте трилатерации 3 и 4 классов определяются два ориентирных направления. Ориентирные пункты закрепляются подземными центрами на расстоянии от 500 до 1000 м (в лесу не ближе 250 м) от основного пункта. Ориентирные пункты должны быть видимы с высоты штатива, установленного над центром пункта, и со столика знака. В качестве одного из ориентирных пунктов может быть принят хорошо видимый до основания геодезический знак или местный предмет (шпиль башни, колокольня и т.п.), находящийся не далее 3 км от пункта сети.
Государственные геодезические сети до их уравнивания должны быть отнесены на поверхность референц-эллипсоида. Для этого в длины линий вводятся поправки за редукцию:
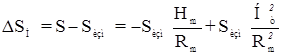 .
.
Для проектирования длины линии на плоскость в проекции Гаусса-Крюгера вычисляют поправку:
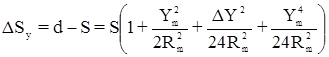 .
.
Окончательно длины линий, отнесенные на поверхность референц-эллипсоида и спроектированные на плоскость в проекции Гаусса-Крюгера, вычисляются по формуле:
D=Sизм + DSH + DSy,
где Sизм – горизонтальное проложение измеренной длины линии.
10.2 Уравнивание сетей трилатерации коррелатным способом
В сети трилатерации измеренными величинами являются длины сторон. Поэтому при уравнивании должны вычисляться поправки к ним, а затем по уравненным длинам сторон – уравненные значения всех параметров сети.
Наиболее простым способом составления условных уравнений является способ сравнения сумм или разностей углов, вычисленных по измеренным длинам сторон с их значениями, полученными по исходным данным.
Углы удобно вычислять по формулам:
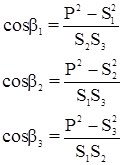 ,
,
где 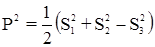 .
.
Подсчет числа условных уравнений выполняется графическим способом с построением схемы сети по длинам ее сторон. При этом каждой избыточной стороне соответствует одно условное уравнений. Для центральной системы трилатерации можно составить лишь одно условное уравнение:
g1 + g2 + g3 + g4 + g5 – 3600 = 0.
Обозначим через g’i углы, вычисленные по измеренным длинам сторон, а поправки к ним – vgi. Тогда:
vg1 + vg2 + vg3 + vg4 + vg5 + w = 0.
где w = g’1 + g’2 + g’3 + g’4 + g’5 – 3600 – свободный член условного уравнения, выраженный в угловой мере.
Поправки в углы vgi зависимы между собой, поэтому для решения условного уравнения необходимо поправки в углы vgi выразить через поправки в измеренные длины сторон vSi и vri. По теореме косинусов запишем:
S1 = r12 + r22 – 2 r1 r2 cos g.
Дифференцируя это выражение, получим:
Дата добавления: 2016-06-02; просмотров: 2709;
