Сущность и задачи уравнивания

В любом геодезическом построении измеряются k необходимых величин, которых достаточно для отыскания неизвестных нам параметров. Например, в сети триангуляции достаточно знать один базис и по два угла в каждом треугольнике сети. Обработав эти измерения, можно получить координаты искомых пунктов.

k = 10 – необходимые измерения;

r = 0 – избыточные измерения;

п = 10

Кроме того, измеряются еще r избыточных (дополнительных) величин. Например, в сети триангуляции измеряются выходной (последний в сети) базис и все третьи углы в треугольниках.

k = 10 – необходимые измерения;

r = 6 – избыточные измерения;

п = 16

Все измерения n = k + r элементов сети сопровождаются погрешностями (случайными и систематическими) и результаты измерений не удовлетворяют математическим соотношениям между ними. Например, сумма измеренных углов в треугольнике отличается от 180⁰.

Элементы геодезического построения связаны между собой различными геометрическими условиями, которые можно записать в виде:

,

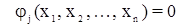где x_i (i = 1, n) – истинные значения элементов сети;

j_j – функциональная зависимость между элементами сети (j = 1, r).

Эти условия называются условными уравнениями связи. При подстановке в условные уравнения измеренных значений х₁, х₂, …, х_п элементов сети получаем невязки:

.

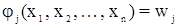Если невязки w_j не превышают допустимого значения, то измерения считаются выполненными правильно, надежно, с достаточной точностью. В этом случае измерения уравниваются для устранения невязок w_j, определения уравненных значений x_i* элементов сети и оценки их точности. Это и является основными задачами уравнивания. По результатам уравнивания вычисленные параметры приобретают лишь одно значение:

,

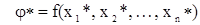а невязки устраняются, т.е.:

.

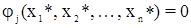Определение поправок в результаты измерений v₁, v₂, …, v_n производится при условии:

.

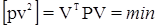Т.е. уравнивание методом наименьших квадратов сводится к отысканию таких поправок в результаты измерений, которые при условии 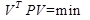дают уравненные значения элементов x_i* = x_i + v_i (i = 1, n).