АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ

Автокорреляционная функция (с. 127)

Автокорреляция остатков (с. 50, 113)

Авторегрессионная модель (с. 132, 136)

Алмон полиномиальные лаги (с. 135)

Вектор остатков (случайных отклонений) (с. 72)

- значений зависимой переменой (с. 71)

Верификация (с. 7)

Вероятность (с. 9)

Временные ряды (с. 6, 124)

Выборка (с. 26)

Гаусса-Маркова условия (предпосылки МНК) (с. 49, 72)

Гетероскедастичность (с. 50, 104, 106)

Гипотеза статистическая (с. 36)

Гомоскедастичность (с. 50)

Двумерная случайная величина (с. 21)

Двухшаговый метод наименьших квадратов (с. 140)

Дисперсия теоретическая (с. 14)

- выборочная (с. 29)

Доверительная вероятность (с. 34)

Доверительный интервал (с. 34)

Идентифицируемость системы одновременных уравнений (с. 147)

Интервальные оценки параметров (с. 54, 56)

Качество уравнения регрессии (с. 42, 70)

Ковариация (с. 23, 30, 75)

Койка преобразование – см. Преобразование Койка (с. 134)

Косвенный метод наименьших квадратов (с. 146)

Коэффициент вариации (с. 14, 30)

Коэффициент детерминации (с. 57, 79)

- скорректированный (с. 80)

Коэффициент корреляции (с. 23, 30)

- межфакторный (парный) (с. 84)

Коэффициент регрессионного уравнения (с. 42, 68)

Лаг (с. 127)

Лаговая переменная (с. 132)

Линеаризация модели (с. 88)

Линия регрессии (модели) (с. 44, 46)

Математическое ожидание случайной величины (с. 13)

Метод взвешенных наименьших квадратов (с. 94, 111)

Метод инструментальных переменных (с. 139, 148)

Метод наименьших квадратов (с. 44, 69)

Модель (с. 5)

- авторегрессионная (с. 132)

- адаптивных ожиданий (с. 132, 136)

- линейная (с. 42, 68)

- множественной регрессии (с. 68)

- нелинейная (с. 89, 90)

- парной регрессии (с. 43)

- регрессионная (с. 42, 68)

- с распределенными лагами (с. 132)

- с автокорреляционными остатками (с. 113)

- с гетероскедастичными остатками (с. 106)

- с распределением Койка (с. 134)

- частичной корректировки (с. 138)

Мультиколлинеарность (с. 69, 82)

Область принятия гипотезы (с. 38)

- отклонения гипотезы (с. 38)

Обобщенный метод наименьших квадратов (с. 104)

Объясненная часть переменной (с. 44)

Остаток (случайное отклонение) (с. 6, 43)

Ошибка

- первого рода (с. 36)

- второго рода (с. 36)

- прогноза (с. 64)

Основные этапы эконометрического моделирования (с. 6)

Параметры эконометрической модели (с. 6, 50)

Переменная зависимая (объясняемая) (с. 42)

- инструментальная (с. 139)

- независимая (объясняющая) (с. 42)

- предопределенная (с. 145)

- фиктивная (с. 93)

- экзогенная (с. 144)

- эндогенная (с. 144)

Плотность вероятности (с. 12)

Прайса-Винстона поправка (с. 119)

Преобразование Койка (с. 134)

Прогнозирование (с. 61)

Распределение случайной величины (с. 15)

- нормальное (с. 16)

- Стьюдента (t-распределение) (с. 18)

- Фишера (F-распределение) (с. 19)

Регрессионная модель

- классическая линейная (с. 51, 69)

- обобщенная (с. 104)

Регрессионный анализ (с. 41, 42)

Регрессия (с. 42)

Регрессор (с. 42)

Сверхидентифицируемость (с. 147)

Сглаживание временных рядов (с. 126)

Сезонная компонента (составляющая) (с. 124)

Система одновременных уравнений (с. 143)

Случайная величина

- дискретная (с. 9)

- непрерывная (с. 10)

Спецификация модели (с. 6, 88)

Среднее квадратическое отклонение (с. 29, 33)

Стандартная ошибка (с. 51-53, 76)

Статистическое определение вероятности (с. 9)

Стационарный временной ряд (с. 125)

Статистика Дарбина-Уотсона (DW) (с. 116)

Степени свободы (с. 18, 55)

Тест (t-тест; F-тест) (с. 55, 59)

- Дарбина-Уотсона (с. 116)

- Голдфелда-Квандта (с. 109)

- ранговой корреляции Спирмена (с. 107)

- Г. Чоу (с. 97)

Тренд временного ряда (с. 124, 131)

Уравнение идентифицируемое (с. 148)

- неидентифицируемое (с. 148)

- регрессионной модели (с. 43, 68)

- структурное (с. 144)

- теоретическое (с. 42)

- эмпирическое (с. 43)

Уровень значимости (с. 36)

Факторный признак (с. 42)

Фиктивная переменная (с. 93)

Функция Кобба-Дугласа (с. 91, 92)

Функция распределения случайной величины

Центральная предельная теорема (с. 24)

Циклическая компонента (с. 124)

Частость (с. 9)

Числовые характеристики (с. 13)

Число степеней свободы (с. 18)

Эконометрика (с. 5)

Эконометрическая модель (с. 5)

Экспоненциальный закон распределения (с. 20)

Эмпирический стандарт (с. 33)

Эффективность оценки (с. 32)

Приложение 1

Функция Лапласа

(стандартизированное нормальное распределение)

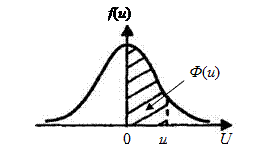
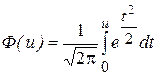
Пример:

Ф(1,65) = Р(0 £ U £ 1,65) = 0,4505;

P(U > 1,65) = 0,4595.

u	,00	,01	,02	,03	,04	,05	,06	,07	,08	,09
0,0	,0000	,0040	,0080	,0120	,0160	,0199	,0239	,0279	,0319	,0359
0,1	,0398	,0438	,0478	,0517	,0557	,0596	,0636	,0675	,0714	,0753
0,2	,0793	,0832	,0871	,0910	,0948	,0987	,1026	,1064	,1103	,1141
0,3	,1179	,1217	,1255	,1293	,1331	,1368	,1406	,1443	,1480	,1517
0,4	,1554	,1591	,1628	,1664	,1700	,1736	,1772	,1808	,1844	,1879
0,5	,1915	,1950	,1985	,2019	,2054	,2088	,2123	,2157	,2190	,2224
0,6	,2257	,2291	,2324	,2357	,2389	,2422	,2454	,2486	,2517	,2549
0,7	,2580	,2611		,2673	,2704	,2734	,2764	,2794	,2823	,2852
	,2881	,2910	,2939	,2967	,2995	,3023	,3051	,3078	,3106	,3133
0,9	,3159	,3186	,3212	,3238	,3264	,3289	,3315	,3340	,3365	,3389
1,0	,3413	,3438	,3461	,3485	,3508	,3531	,3554	,3577	,3599	,3621
1,1	,3643	,3665	,3686	,3708	,3729	,3749	,3770	,3790	,3810	,3830
1,2	,3849	,3869	,3888	,3907	,3925	,3944	,3962	,3980	,3997	,4015
1,3	,4032	,4049	,4066	,4082	,4099	,4115	,4131	,4147	,4162	,4177
1,4	,4192	,4207	,4222	,4236	,4251	,4265	,4279	,4292	,4306	,4319
1,5	,4332	,4345	,4357	,4370	,4382	,4894	,4406	,4418	,4429	,4441
1,6	,4452	,4463	,4474	,4484	,4495	,4505	,4515	,4525	,4535	,4545
1,7	,4554	,4564	,4573	,4582	,4591	,4599	,4608	,4616	,4625	,4633
1,8	,4641	,4649	,4656	,4664	,4671	,4678	,4686	,4693	,4699	,4706
1,9	,4713	,4719	,4726	,4732	,4738	,4744	,4750	,4756	,4761	,4767
2,0	,4772	,4778	,4783	,4788	,4793	,4798	,4803	,4808	,4812	,4817
2,1	,4821	,4826	,4830	,4834	,4838	,4842	,4846	,4850	,4854	,4857
2,2	,4861	,4864	,4868	,4871	,4875	,4878	,4881	,4884	,4887	,4890
2,3	,4893	,4896	,4898	,4901	,4904	,4906	,4909	,4911	,4913	,4916
2,4	,4918	,4920	,4922	,4925	,4927	,4929	,4931	,4932	,4934	,4936
2,5	,4938	,4940	,4941	,4943	,4945	,4946	,4948	,4949	,4951	,4952
2,6	,4953	,4955	,4956	,4957	,4959	,4960	,4961	,4962	,4963	,4964
2,7	,4965	,4966	,4967	,4968	,4969	,4970	,4971	,4972	,4973	,4974
2,8	,4974	,4975	,4976	,4977	,4977	,4978	,4979	,4979	,4980	,4981
2,9	,4981	,4982	,4982	,4983	,4984	,4984	,4985	,4985	,4986	,4986
3,0	,4987	,4987	,4987	,4988	,4988	,4989	,4989	,4989	,4990	,4990

3,1 ,49903 3,2 ,49931 3,3 ,49952 3,4 ,49966 3,5 ,49977 3,6 ,49984 3,7 ,49989

3,8 ,49993 3,9 ,49995 4,0 ,499968 4,5 ,49999 5,0 ,49999997

Приложение 2

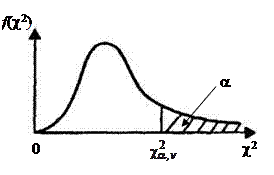c²-распределение

Пример:

при v = 15 Р(c² > 8,55) = 0,9,

Р(c² > 22,31) = 0,1;

при v > 100 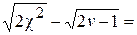U(U ~ N(0,1)).

a v	,995	,990	,975	,950	,900	,750	,500	,250	,100	,050	,025	,010	,005
	,4×10^-6	,2×10^-5	10-5	4×10^-4	,016	,101	,454	1,32	2,71	3,84	5,02	6,63	7,88
	,010	,020	,051	,103	,211	,58	1,39	2,77	4,61	5,99	7,38	9,21	10,60
	,072	,115	,216	,352	,584	1,21	2,37	4,11	6,25	7,81	9,35	11,34	12,84
	,207	,297	,484	,711	1,06	1,92	3,36	5,39	7,78	9,49	11,14	13,28	14,86
	,412	,554	,831	1,15	1,61	2,67	4,35	6,63	9,24	11,07	12,83	15,09	16,75
	,676	,872	1,24	1,64	2,20	3,45	5,35	7,84	10,64	12,59	14,45	16,81	18,55
	,989	1,24	1,69	2,17	2,83	4,25	6,35	9,04	12,02	14,07	16,01	18,48	20,28
	1,34	1,65	2,18	2,73	3,49	5,07	7,34	10,22	13,37	15,51	17,53	20,09	21,96
	1,73	2,09	2,70	3,33	4,17	5,90	8,34	11,39	14,68	16,92	19,02	21,67	23,59
	2,16	2,56	3,25	3,94	4,87	6,74	9,34	12,55	15,99	18,31	20,48	23,21	25,19
	2,60	3,05	3,82	4,57	5,58	7,58	10,34	13,70	17,28	19,68	21,92	24,73	26,76
	3,07	3,57	4,40	5,23	6,30	8,44	11,34	14,85	18,55	21,03	23,34	26,22	28,30
	3,57	4,11	5,01	5,89	7,04	9,30	12,34	15,98	19,81	22,36	24,74	27,69	29,19
	4,07	4,66	5,63	6,57	7,79	10,1	13,34	17,12	21,06	23,69	26,12	29,14	31,32
	4,60	5,23	6,26	7,26	8,55	11,04	14,34	18,25	22,31	25,00	27,49	30,58	32,80
	5,14	5,81	6,91	7,96	9,31	11,91	15,34	19,37	23,54	26,30	28,85	32,00	34,27
	5,68	6,41	7,56	8,67	10,09	12,79	16,34	20,49	24,77	27,59	30,19	33,41	35,72
	6,26	7,01	8,23	9,39	10,86	13,68	17,34	21,60	25,99	28,87	31,53	34,81	37,16
	6,84	7,63	8,91	10,12	11,65	14,56	18,34	22,72	27,20	30,14	32,85	36,19	38,58
	7,43	8,26	9,59	10,85	12,44	15,45	19,34	23,88	28,41	31,41	34,17	37,57	40,00
	8,03	8,90	10,28	11,59	13,24	16,34	20,34	24,93	29,61	32,67	35,48	38,93	41,40
	9,26	10,20	11,69	13,09	14,85	18,14	21,34	26,04	30,81	33,92	36,78	40,29	42,80
	9,89	10,86	12,40	13,85	15,66	19,04	22,34	27,14	32,01	35,17	38,08	41,64	44,18
	8,64	9,54	10,98	12,34	14,04	17,24	23,34	28,24	33,20	36,42	39,36	42,98	45,56
	10,52	11,52	13,12	14,61	16,47	19,94	24,34	29,34	34,38	37,65	40,65	44,31	46,93
	11,16	12,20	13,84	15,38	17,29	20,84	25,34	30,43	35,56	38,89	41,92	45,64	48,29
	11,81	12,88	14,57	16,15	18,11	21,78	26,34	31,53	36,74	40,11	43,19	46,96	49,64
	12,46	13,56	15,31	16,93	18,94	22,66	27,34	32,62	37,92	41,34	44,46	48,28	50,99
	13,12	14,26	16,05	17,71	19,77	23,57	28,34	33,71	39,09	42,56	45,72	49,59	52,34
	13,78	14,95	16,79	18,49	20,60	24,48	29,34	34,80	40,26	43,77	46,98	50,89	53,67
	20,71	22,16	,24,43	26,51	29,05	33,66	39,34	45,62	51,81	55,76	59,34	63,69	66,77
	27,99	29,70	32,36	34,76	37,69	42,94	49,33	56,33	63,17	67,50	71,42	76,15	79,49
	35,53	37,48	40,48	43,19	46,46	52,29	59,33	66,98	74,38	79,08	83,30	88,38	91,95
	43,28	45,44	48,76	51,74	55,33	61,70	69,33	77,58	85,53	90,53	95,02	100,4	104,2
	51,17	53,54	57,15	60,39	64,28	71,14	79,33	88,13	96,58	101,9	106,6	112,3	116,3
	59,20	61,75	65,65	69,13	73,29	80,62	89,33	98,65	107,6	113,1	118,1	124,1	128,3
	67,32	70,06	74,22	77,93	82,36	90,13	99,33	109,1	118,5	124,3	129,6	135,8	140,2

Приложение 3

<2 3 4 5 678 >

Дата добавления: 2016-06-02; просмотров: 1052;