Оценка моделей с распределенными лагами

Методы оценки моделей с распределенными лагами в независимых переменных во многом определяются тем, конечное или бесконечное число лагов содержит соответствующее регрессионное уравнение.

Модель, описываемая уравнением

(6.13)

с конечным числом лагов k (максимальный лаг определяет порядок модели), оценивается достаточно просто путем сведения ее к уравнению множественной регрессии. В этом случае, полагая в (6.13) Х₀ = х_t, Х₁ = х_{t - 1}, …, Х_k = х_{t - k}, получают уравнение:

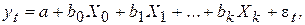(6.14)

оценка параметров которого может быть произведена по МНК. Возможные трудности при оценивании подобных моделей могут быть связаны с проявлением мультиколлинеарности или автокорреляции.

В модели с бесконечным числом лагов, теоретическое уравнение которой имеет вид:

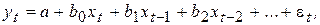(6.15)

предполагается, что влияние переменной Х не заканчивается в момент времени k, а продолжается бесконечно, убывая по определенному закону. Подобные модели встречаются на практике и имеют достаточно ясный экономический смысл, так как логично предположить, что влияние прошлых значений объясняющих переменных на текущее значение зависимой переменной будет тем меньше, чем дальше по времени наблюдались эти показатели. Отметим, что в моделях (6.14) и (6.15) коэффициент b₀ называют краткосрочным мультипликатором в силу того, что он характеризует изменение среднего значения переменной Y под воздействием единичного изменения переменной Х в тот же самый период времени.

Для модели с бесконечным числом лагов можно применить распределение Койка, в котором принимается, что коэффициенты (или «веса») b_k при лагированных переменных убывают с каждым шагом по времени в геометрической прогрессии:

b_k = b₀l^k, k = 0, 1, 2, …, (6.16)

где параметр l(0 < l < 1) характеризует скорость убывания коэффициентов с увеличением лага. Тогда модель (6.15) преобразуется в уравнение:

(6.17)

Модель (6.17) содержит теперь только три параметра (a, b₀, l), однако ее оценивание затруднено тем, что она является нелинейной.

Наиболее часто для определения параметров уравнения (6.17) используется процедура, которая называется нелинейным методом наименьших квадратов. Эта процедура реализуется в большинстве компьютерных эконометрических пакетов. Сущность метода заключается в следующем.

1. С достаточно мелким фиксированным шагом (например, 0,01 или 0,001) перебираются все значения l из интервала (0, 1).

2. Для каждого значения l рассчитывается величина:

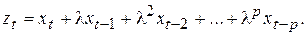(6.18)

Значение р (предел суммирования) определяется из условия, что дальнейшие члены ряда вносят в его сумму незначительный вклад.

3. Для каждого z по МНК оценивается уравнение:

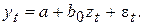(6.19)

4. Выбирается то уравнение (6.19), которое обеспечивает наибольший коэффициент детерминации R². Соответствующее значение 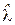принимается за оценку параметра l. Найденные оценки a, b₀ и l подставляются в (6.17).

Другой способ оценивания состоит в преобразовании уравнения (6.17) в авторегрессионное уравнение. Для этого из уравнения (6.17) вычитается то же самое уравнение, сдвинутое по времени на один шаг назад и умноженное на l. В результате получим следующее выражение:

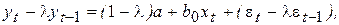
или

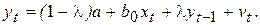(6.20)

Здесь v_t = e_t - le_{t - 1} (t = 1, …, n) представляет собой скользящую среднюю между e_t и e_{t - 1}. Проведенное преобразование позволило избавиться от бесконечного числа лаговых переменных. С помощью МНК мы можем оценить параметры полученной двухфакторной регрессионной модели. При оценивании уравнения (6.20) следует учитывать возможное проявление автокорреляции для случайных отклонений v_t, а также появление в модели, в качестве регрессора, переменной у_{t - 1}, которая, в принципе, носит случайный (стохастический) характер. Поэтому оценки параметров l, a и b₀ могут обладать недостатками, связанными с нарушением условий классической регрессионной модели.

В модели геометрических лагов Койка на коэффициенты регрессии накладываются достаточно сильные ограничения, которые в ряде случаев могут не выполняться. Так, например, встречаются ситуации, когда значения лаговой объясняющей переменной за 3–4 периода от момента наблюдения оказывают на зависимую переменную большее влияние, чем текущее или предшествующее ему значение регрессора (b₃, b₄ > b₀, b). В таких случаях следует применять модели полиномиальных лагов Алмон, которые достаточно гибко отражают изменения в поведении лаговых объясняющих переменных.

В основе модели Алмон лежит предположение, что «веса» коэффициентов b_i в уравнении (6.13) аппроксимируются полиномами определенной степени от величины лага i:

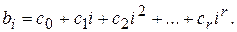(6.21)

Для простоты изложения метода Алмон будем считать, что b_i определяется квадратичной зависимостью:

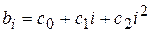. (6.22)

Тогда уравнение (6.13) после подстановки (6.22) может быть представлено в виде:

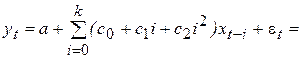
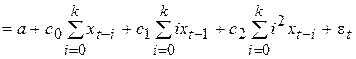. (6.23)

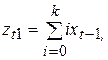
Полагая, что 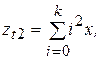получим уравнение:

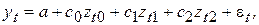(6.24)

параметры которого a, с₀, с₁ и с₂ могут быть оценены по МНК. Затем коэффициенты b_i определяются из соотношения (6.22).

В общем случае модель полиномиальных лагов Алмон содержит только r + 2 неизвестных параметров, где r - степень полинома. Для эффективного применения метода Алмон рекомендуется вначале определиться с количеством лагов k и подобрать степень полинома r, описывающего структуру лага. Проверка адекватности модели может быть проведена на основе обычной F-статистики (см. раздел 3.3.2).