Энергия математического маятника

Автор: Смогли бы Вы определить кинетическую, потенциальную и полную энергию математического маятника, если известно, что его масса т, длина l, и он совершает колебания с амплитудой а.

Читатель: Если мы знаем l, значит, знаем и 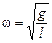. Пусть маятник колеблется по закону: х = аcoswt, тогда его проекция скорости изменяется по закону

υ_х = х¢(t) = –аwsinwt.

Тогда кинетическая энергия равна

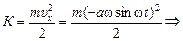
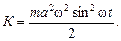(3.7)

Автор: Верно. А как найти полную энергию?

Читатель: Я думаю, что она равна максимальному значению кинетической энергии:

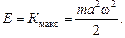(3.8)

Автор: Верно. Осталось найти потенциальную энергию.

Читатель: Поскольку П + К = Е, то

П = Е – К =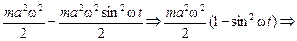

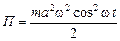. (3.9)

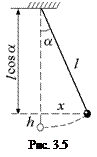Автор: Я согласен с Вами. Но вот какой вопрос меня беспокоит: потенциальная энергия математического маятника, по идее, должна быть равна mgh, где h – высота подъема над положением равновесия (рис. 3.5).

Тогда потенциальная энергия маятника, отклоненного от положения равновесия на угол a, должна быть равна

П = mgl(1 – cosa). (3.10)

Как это согласовать с формулой (3.9)?

Читатель: Странно… Формулы вроде бы раз-

ные…

Автор: Но если мы с Вами вспомним, что при малых углах a справедлива формула (3.1): cosa » 1 – 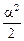, то…

Читатель: Тогда П » mgl .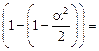

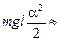
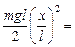
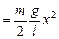
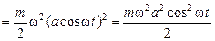Действительно, все совпадает!

Автор: Замечательно! Но следует помнить, что все наши формулы для математического маятника приближенные и «работают» только при малых углах.

СТОП! Решите самостоятельно: А7, А8, В8.

Автор: Как Вы думаете, изменится ли период колебаний математического маятника, если, кроме силы тяжести, на него действуют еще какие-нибудь силы – электрические или магнитные?

Читатель: Я думаю, да. Если силы будут направлены вниз, то получится, что g как бы увеличивается, а если вверх – то уменьшается. Если g увеличивается, то Т уменьшается, а если g уменьшается, то Т увеличивается согласно формуле (3.5).

СТОП! Решите самостоятельно: А9, А10.