Задачи средней трудности. В1. Какова частота колебаний поршней в цилиндрах двигателя автомобиля «Жигули» при скорости движения автомобиля 120 км/ч
В1. Какова частота колебаний поршней в цилиндрах двигателя автомобиля «Жигули» при скорости движения автомобиля 120 км/ч, если диаметр колес 60 см и частота вращения коленчатого вала в 4,3 раза больше частоты вращения колес?
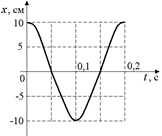 Рис. 1.8
Рис. 1.8
|
В2. Уравнение движения гармонического колебания имеет вид: х = 0,02cospt. Построить график зависимости х(t). Найти смещение через 0,25 с; через 1,25 с. Ответы пояснить с помощью графика.
В3. При каких фазах смещение по модулю равно половине амплитуды?
В4. По графику, приведенному на рис. 1.8: а) найти амплитуду, период, частоту и циклическую частоту колебаний; б) написать уравнение зависимости х(t); в) найти смещение колеблющейся точки при фазах p/2 и 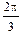 рад; г) найти смещение через 0,1 и 0,15 с после начала отсчета времени.
рад; г) найти смещение через 0,1 и 0,15 с после начала отсчета времени.
В5. Амплитуда колебаний 10 см, в частота 0,5 Гц. Написать уравнение зависимости х(t) и построить его график. Найти фазу и смещение через 1,5 с. Определить, через сколько времени смещение будет 7,1 см.
В6. При фазе p/3 рад смещение было равно 1 см. Найти амплитуду колебаний и смещение при фазе 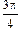 рад.
рад.
В7. Составить уравнение гармонического колебания, если амплитуда колебания 4 см, а период – 0,01 с, х0 = 0. колебания происходят по закону х = acos(wt + a).
В8. Колебательное движение точки описывается уравнением х = =0,05cos20pt. Вычислив первую и вторую производные, написать уравнения зависимости скорости и ускорения от времени: υх(t) и ax(t). Найти координату, скорость и ускорение спустя 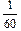 с после момента t = 0.
с после момента t = 0.
В9. Амплитуда колебаний конца ножки камертона 1 мм, а частота колебаний 500 Гц. Написать уравнения х(t), υх(t) и ax(t). Каковы наибольшие значения скорости и ускорения? В каких положениях достигаются эти значения?
В10. Написать уравнение гармонического колебания тела, если его амплитуда 5 см, период 4 с, начальная фаза равна p/4, а также зависимости υх(t) и ax(t). колебания происходят по закону х = acos(wt + a).
В11. Тело совершает колебания по закону х = 0,3cosp(t + 0,5) м. Найти амплитуду, период, начальную фазу колебаний и ускорение в момент времени t = 0,5 с.
В12. Человек массой 80 кг качается на качелях. Амплитуда его колебания 1 м. За 1 мин он совершает 15 колебаний. Найти кинетическую и потенциальную энергию через 1/12 периода.
В13. Материальная точка массой 10 г колеблется по закону х = =0,05sin(0,6t + 0,8). Найти максимальную силу, действующую на точку, и полную энергию колеблющейся точки.
Задачи трудные
С1. Сравнить время прохождения колеблющейся точкой первой и второй половины амплитуды: t1 : t2 = ? Начальное смещение равно амплитуде х(0) = а.
С2. Какую часть периода груз маятника находится в пределах 1 см от положения равновесия, если амплитуда его колебания равна 2 см?
С3. Шарик массой 10 г совершает гармонические колебания с амплитудой А = 0,2 м и периодом Т = 4 с. В момент t0 = 0 х = А. Найти кинетическую и потенциальную энергии в момент времени t = 1 с.
С4. Написать уравнение гармонического колебания тела, если его полная энергия 3×10–5 Дж, максимальная сила, действующая на тело, 1,5 мН, период колебания 2 с и начальная фаза 60°. колебания происходят по закону х = acos(wt + p/3).
Пружинный маятник
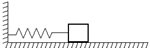
Автор: Рассмотрим такую задачу. На гладкой поверхности лежит груз массой т, прикрепленный к стене пружиной жесткостью k (рис. 2.1). Как будет двигаться груз, если его слегка отвести в сторону и отпустить?
| 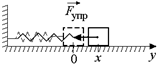
|
Рис. 2.1 Рис. 2.2
Читатель: По-моему, возникнет ситуация, абсолютно аналогичная той, что мы рассмотрели в § 1: на груз начнет действовать сила упругости, которая по закону Гука прямо пропорциональна смещению х и направлена к положению равновесия, причем Fx = –kx (рис. 2.2).
Автор: Совершенно верно! А сила упругости в данном случае будет играть роль той самой квазиупругой «возвращающей» силы, которую мы ввели в рассмотрение в § 1!
Читатель: Но тогда для нашего груза будут справедливы все полученные в § 1 результаты: он будет колебаться по закону
х = acoswt,
где а – амплитуда, а 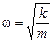 – циклическая частота. (Я учел, что начальная фаза равна нулю: a = 0.)
– циклическая частота. (Я учел, что начальная фаза равна нулю: a = 0.)
Автор: Верно! А каков будет период колебаний?
Читатель: 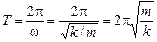 .
.
Автор: Эту формулу надо запомнить:
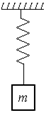 Рис. 2.3
Рис. 2.3
| 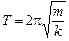 . (2.1)
Теперь у меня следующий вопрос: а как изменится период колебаний, если груз повесить на той же пружине, как показано на рис. 2.3?
Читатель: Здесь надо будет учесть действие силы тяжести: в положении равновесия пружина будет растянута, должно выполняться равенство mg = Fупр. А что касается периода колебаний…, даже не знаю… . (2.1)
Теперь у меня следующий вопрос: а как изменится период колебаний, если груз повесить на той же пружине, как показано на рис. 2.3?
Читатель: Здесь надо будет учесть действие силы тяжести: в положении равновесия пружина будет растянута, должно выполняться равенство mg = Fупр. А что касается периода колебаний…, даже не знаю…
|
Автор: Вы правы. Если груз подвешен на пружине, то, помимо силы упругости, на его колебания будет влиять сила тяжести. Но ее действие можно исключить из рассмотрения таким приемом.
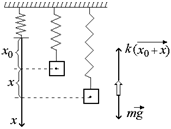 Рис. 2.4
Рис. 2.4
|
Пусть в положении равновесия пружина удлинилась на расстояние х0от недеформированного положения (рис. 2.4). Ясно, что в положении равновесия mg = kx0. Если пружину растянуть еще на расстояние х, считая от этой точки, то проекция равнодействующей всех сил, приложенных к грузу на ось х, будет равна
 Fx = –k(х0 + х)+ mg = –kх0 – kх + mg = (mg – kx0) 0– kx = –kx.
Fx = –k(х0 + х)+ mg = –kх0 – kх + mg = (mg – kx0) 0– kx = –kx.
Таким образом, если начало координат поместить в точку, соответствующую положению равновесия, то все будет происходить так, как если бы на груз действовала только упругая сила пружины Fx = –kх. А значит, период колебаний не изменится.
Задача 2.1. Пружинный маятник колеблется с периодом Т = = 1,0 с. Масса груза т = 1,0 кг. Какова жесткость пружины?
| Т = 1,0 с т = 1,0 кг | Решение. Согласно формуле (2.1)
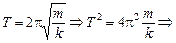
|
| k = ? |
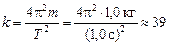 Н/м.
Н/м.
Ответ: 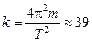 Н/м.
Н/м.
СТОП! Решите самостоятельно: А1–А3, В1, С1, С3.
Задача 2.2. Найти проекции ускорения шарика (рис. 2.5) при смещениях х1 = 2,0 см и х2 = –0,50 см, если масса шарика т = 100 г и жесткость пружины k = 400 Н/м. В какой точке проекция ускорения равна 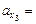 10 м/с2?
10 м/с2?
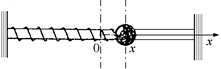 Рис. 2.5
Решение. Воспользуемся вторым законом Ньютона в проекции на ось х:
тах = –kx Þ ax = –
Рис. 2.5
Решение. Воспользуемся вторым законом Ньютона в проекции на ось х:
тах = –kx Þ ax = – 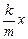 . .
| |
х1 = 2,0 см
х2 = –0,50 см
т = 100 г = 0,100 кг
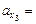 10 м/с2
k = 400 Н/м 10 м/с2
k = 400 Н/м
| |
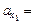 ? ? 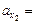 ? х3 = ? ? х3 = ?
| |
Тогда
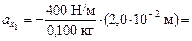 –80 м/с2,
–80 м/с2,
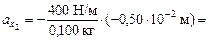 20 м/с2,
20 м/с2,
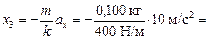 –0,25×10–2 м = –0,25 см.
–0,25×10–2 м = –0,25 см.
Ответ: 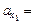 –80 м/с2;
–80 м/с2; 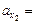 20 м/с2; х3 = –0,25 см.
20 м/с2; х3 = –0,25 см.
СТОП! Решите самостоятельно: В2, В3, С2.
Задача 2.3. Груз, подвешенный на пружине с жесткостью 1,0 кН/м, колеблется с амплитудой 2,0 см. Найти кинетическую и потенциальную энергию при фазе p/3 рад.
| k = 1,0 кН/м = 1,0×103 Н/м а = 2,0 см = 2,0×10–2 м j = p/3 рад | Решение. Потенциальная энергия сжатой или растянутой пружины 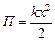 . Если х = аcoswt или (если учесть, что фаза j = wt) х = аcosj, то . Если х = аcoswt или (если учесть, что фаза j = wt) х = аcosj, то
|
| К = ? П = ? | |
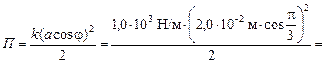 5,0×10–2 Дж.
5,0×10–2 Дж.
Полная энергия Е равна максимальному значению потенциальной энергии, то есть Е = П в тот момент, когда груз находится в крайнем положении, а его смещение равно амплитуде: 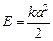 . Поскольку полная энергия равна сумме потенциальной и кинетической энергий, то
. Поскольку полная энергия равна сумме потенциальной и кинетической энергий, то
Е = П + К Þ К = Е – П Þ
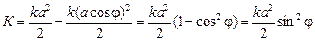 .
.
Подставим численные значения:
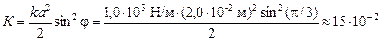 Дж.
Дж.
Ответ: 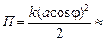 5,0×10–2 Дж;
5,0×10–2 Дж; 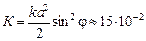 Дж.
Дж.
СТОП! Решите самостоятельно: В4, В5, С3.
Задача 2.4. Тело массой т подвешено на двух пружинах одинаковой длины, но с разными упругими свойствами. Коэффициенты упругости k1 и k2. Определите частоту колебаний тела в случаях а и б (рис. 2.6).
| k1 k2 т | Решение. Поставим вопрос так: пружинами какой жесткости k01 и k02 можно заменить эти системы пружин, чтобы при одинаковой внешней силе F они деформировались на такую же величину Dl? 1. Растянем две параллельные пружины на величину Dl, тогда общая сила, действующая на груз, будет равна |
| n1 = ? n2 = ? |
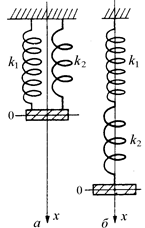 Рис. 2.6
Рис. 2.6
|
F = F1 + F2 = k1Dl + k2Dl. (1)
С другой стороны, при замене этих двух пружин на одну жесткостью k01 получим
F = k01Dl . (2)
Приравнивая правые части равенств (1) и (2), получим
k1Dl + k2Dl = k01Dl Þ k01 = k1 + k2.
Запомним: при параллельном соединении жесткость эквивалентной пружины равна сумме жесткостей соединенных пружин:
k01 = k1 + k2. (2.2)
Тогда частота колебаний будет равна
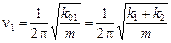 .
.
2. Растянем две последовательно соединенные пружины так, чтобы общее удлинение было равно Dl. Тогда первая пружина удлинится на Dl1, а вторая – на Dl2, но при этом
Dl1 + Dl2 = Dl. (3)
Заметим, что в этом случае силы натяжения обеих пружин одинаковы:
F = k1Dl1 = k2Dl2 (4)
(иначе система не находилась бы в равновесии).
При замене этих двух пружин на эквивалентную, жесткостью k02, сила F будет равна
F = k02Dl. (5)
Выразим величины Dl1 и Dl2 из (4), а Dl из (5) и подставим в (3), получим
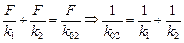 .
.
Запомним: при последовательном соединении пружин справедливо
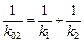 . (2.3)
. (2.3)
Из (2.2) выразим k02:
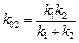 . (2.4)
. (2.4)
Теперь найдем частоту колебаний для случая последовательного соединения пружин:
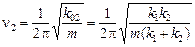 .
.
Ответ: 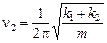 ;
; 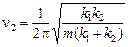 .
.
Автор: Как Вы думаете, чему будет равна жесткость пружины, составленной из п маленьких одинаковых пружин жесткостью k, соединенных последовательно?
Читатель: Если обобщить формулу (2.2) для произвольного п (по-моему, это нетрудно сделать), то получим
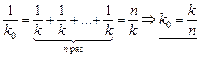 .
.
Автор: Совершенно верно! Жесткость большой пружины будет меньше жесткости каждой маленькой пружины в п раз.
СТОП! Решите самостоятельно: А4, В6, В7.
Дата добавления: 2016-04-11; просмотров: 8069;
