Самые «простые» колебания
Гармонические колебания
Что такое механические колебания?
Под механическими колебаниями мы понимаем процесс, обладающий той или иной степенью повторяемости. Например, колеблется вода в стакане, колеблется груз, подвешенный на пружине, колеблется автомобиль на рессорах, колеблются качели, колеблется зажатая одним концом металлическая пластина, колеблется натянутая струна, колеблется стрелка компаса (рис. 1.1).

Рис. 1.1
Совершают колебания также молоток, висящий на гвозде, весы, груз на веревке, маятник часов (рис. 1.2).
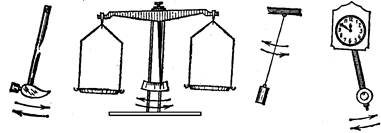
Рис. 1.2
Самые «простые» колебания
Начнем с самых простых колебаний – гармонических. Говорят, что точка совершает гармонические колебания вдоль оси х, если ее координата изменяется по закону:
х(t) = acos(wt + a), (1.1)
где t – время, а а, a, w – постоянные величины, с физическим смыслом которых мы разберемся чуть позже.
 Рис. 1.3
Рис. 1.3
|
График зависимости х(t) представляет собой синусоиду (рис. 1.3).
Выясним, в каких случаях возникают именно гармонические (а не какие-либо другие) колебания.
Рассмотрим такую систему: вдоль оси х может двигаться без трения материальная точка массой т. При этом в нулевой точке на нее никакие силы не действуют, а в случае смещения в точку с координатой х на нее начинает действовать «возвращающая» сила, проекция которой на ось х равна
 Рис. 1.4
Рис. 1.4
|
Fx = – kx, (1.2)
где k – постоянная величина (рис. 1.4).
Эту силу еще называют квазиупругой. Она обладает двумя свойствами: 1) всегда направлена к точке равновесия – нулевой точке на оси х; 2) линейно зависит от величины координаты х.
Так вот, если материальная точка оказывается под действием только квазиупругой силы, то она начинает совершать гармонические колебания по закону (1.1).
Читатель: То, что под действием квазиупругой силы материальная точка начнет колебаться, в общем понятно. Но вот почему эти колебания будут проходить именно по гармоническому закону – совершенно непонятно.
Автор: Давайте докажем это строго.
Прежде всего, вспомним, что если координата точки изменяется по закону х = х(t), то проекция скорости на ось х равна производной функции х(t) по времени: υх = х′(t). А проекция ускорения точки на ось х равна производной проекции скорости на ось х:
ах =  .
.
То есть проекция ускорения – это вторая производная координаты по времени.
Пусть в некоторый момент времени t материальная точка имеет координату х(t). Тогда на нее действует квазиупругая сила, проекция которой на ось х равна
Fx = –kx(t). (1)
С другой стороны, по второму закону Ньютона
Fx = max = mx′′(t). (2)
Приравнивая правые части равенств (1) и (2), получим:
– kx(t) = mx′′(t)
или
x′′(t) +  . (1.3)
. (1.3)
Теперь наша задача состоит в том, чтобы доказать, что функция x(t) = acos(wt + a) удовлетворяет уравнению (1.3). Вычислим вторую производную этой функции. Сначала вычислим первую производную:

Запомним:
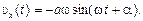 (1.4)
(1.4)
Вычислим вторую производную:
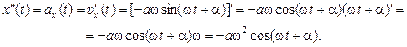
Запомним:
 . (1.5)
. (1.5)
Теперь подставим значения х(t) и х″(t) в формулу (1.3), получим:
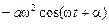 +
+  Þ
Þ
Þ 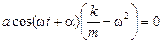 .
.
Это равенство выполняется при любом значении t, если выражение, стоящее скобках, равно нулю:

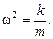 (1.6)
(1.6)
Итак, мы доказали, что функция х(t) = 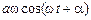 удовлетворяет уравнению (1.3) при условии
удовлетворяет уравнению (1.3) при условии 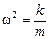 и любых значениях констант а и a. Кстати, мы определили w – одну из трех констант, входящих в функцию х(t) =
и любых значениях констант а и a. Кстати, мы определили w – одну из трех констант, входящих в функцию х(t) = 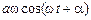 :
:
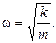 (1.6а)
(1.6а)
Читатель: А как определить остальные две: а и a?
Автор: Они определяются начальными условиями: значениями υх и х в момент начала движения t = t0. Найдем их для частного случая, когда материальная точка в момент t = 0 находится в точке с координатой х = х0 и имеет нулевую начальную скорость υх(0) = 0. Тогда
х(0) = х0 = аcos(w×0 + a) = аcosa.
Согласно формуле (1.4)
υх(0) = 0 = – аsin(w×0 + a) = –asina;
 , х0 = a×cos0 = a×1 Þ а = х0.
, х0 = a×cos0 = a×1 Þ а = х0.
(мы взяли только одно из возможных решений уравнения sina = 0). Теперь наша функция х(t) примет вид
х(t) = х0coswt. (1.7)
Читатель: Но здесь возникает еще один вопрос: а где гарантия, что х(t) = а0cos(wt + a) – единственное решение уравнения (1.3)?
Автор: На этот вопрос можно ответить двояко. С чисто математической точки зрения, можно сослаться на то, что существует строгое доказательство единственности решения уравнений типа (1.3). (Кстати, такие уравнения называются линейными дифференциальными уравнениями второго порядка с постоянными коэффициентами.) С чисто физической точки зрения, единственность решения очевидна: если мы поставим два тела в абсолютно одинаковые начальные условия, а потом будем действовать на них абсолютно одинаковыми силами, то эти тела должны совершать абсолютно одинаковые движения. Правда, оговорюсь, что это очевидно только в классической механике.
Дадим четкие определения введенным нами величинам.
Величина х(t) называется смещением.
Величина а в формуле х(t) = аcos(wt + a) называется амплитудой колебания и показывает величину максимального смещения; а – величина положительная.
Величина w называется циклической частотой колебания и измеряется как угловая скорость в радианах в секунду: [w] = рад/с.
Величина аргумента косинуса (wt + a) называется фазой колебания.
Величина a называется начальной фазой.
Периодом колебания Т называется минимальное время, через которое точка совершит одно полное колебание. Так как период функции косинус равен 2p, то из этого следует, что в момент времени (t + Т) фаза должна быть больше фазы в момент времени t на 2p:
w(t + T) + a = (wt + a) + 2p Þ wT =2p Þ
 . (1.8)
. (1.8)
Частотой колебания n называют величину, которая показывает число колебаний, совершенных за единицу времени. Так, если за время t совершено п колебаний, то
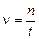 , [n] = 1/с = Гц (герц).
, [n] = 1/с = Гц (герц).
Если п = 1, то t = T, тогда
 . (1.9)
. (1.9)
Задача 1.1. Материальная точка совершает гармонические колебания по закону х(t) = 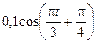 . Определите амплитуду а, циклическую частоту w, частоту n, период Т, начальную фазу a, а также путь s, пройденный за один период[1].
. Определите амплитуду а, циклическую частоту w, частоту n, период Т, начальную фазу a, а также путь s, пройденный за один период[1].
х(t) = 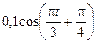
| Решение. Сравним заданное уравнение с уравнением гармонических колебаний:
х(t) = 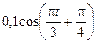 , х(t) = аcos(wt + a). , х(t) = аcos(wt + a).
|
| а = ? w = ? n = ? Т = ? a = ? s = ? | |
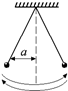 Рис. 1.5
Рис. 1.5
|
Очевидно, что а = 0,1 м, w = p/3 рад/с, a = p/4.
Согласно формуле (1.9) 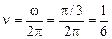 Гц.
Гц.
Согласно формуле (1.8)  6 с.
6 с.
Осталось найти путь, пройденный за период. Из рис. 1.5 видно, что s = 4а = 4×0,1 м = 0,4 м.
Ответ: а = 0,1 м; w = p/3 рад/с; n = 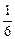 Гц; a = p/4; Т = 6 с; s = 0,4 м.
Гц; a = p/4; Т = 6 с; s = 0,4 м.
СТОП! Решите самостоятельно: А1–А4, В1.
Задача 1.2.Материальная точка совершает колебания по закону х(t) = 2cos  . Определить смещение в моменты t1 = 1 с и t2 = 1,5 с, а также моменты времени, в которые х3 =
. Определить смещение в моменты t1 = 1 с и t2 = 1,5 с, а также моменты времени, в которые х3 = 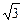 м. Движение рассматривается в течение одного периода.
м. Движение рассматривается в течение одного периода.
х(t) = 2cos  , х3 = , х3 = 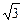 м
t1 = 1 с, t2 = 1,5 с м
t1 = 1 с, t2 = 1,5 с
| Решение.
х1 = 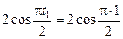 = 0; = 0;
|
| х1 = ? х2 = ? t3 = ? |
х2 = 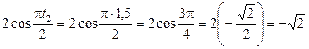 м;
м;
х3 = 
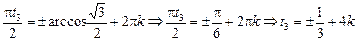 .
.
Если k = 0, то  с; если k = 1, то
с; если k = 1, то 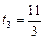 с и
с и 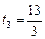 с. К первому периоду относятся значения
с. К первому периоду относятся значения 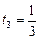 с и
с и  с.
с.
Ответ: х1 = 0; х2 = – 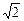 м;
м; 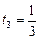 с и
с и  с.
с.
СТОП! Решите самостоятельно: А5, В2–В7, С1, С2.
Задача 1.3. Написать уравнение гармонического колебания, амплитуда которого 10 см, период 10 с, начальная фаза равна нулю. Найти смещение, проекции скорости и ускорения колеблющегося тела через 12 с после начала колебаний.
| а = 0,1 м Т = 10 с, t1 = 12 с a = 0 | Решение. Согласно формуле (1.8)
 рад/с.
Запишем уравнение колебаний рад/с.
Запишем уравнение колебаний
|
| х(t1) = ? υх(t1) = ? ах(t1) = ? |
х(t) = аcos(wt + a) =  .
.
Тогда
х(t1) =  0,031 м;
0,031 м;
υх(t) = 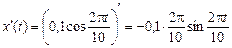 ;
;
υх(t1) = 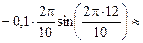 –0,060 м/с;
–0,060 м/с;
ах(t) =  ;
;
ах(t1) = 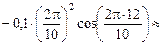 –0,012 м/с2.
–0,012 м/с2.
Ответ: х(t1) » 0,031 м; υх(t1) » –0,060 м/с; ах(t1) » –0,012 м/с2.
СТОП! Решите самостоятельно: В8–В11.
Дата добавления: 2016-04-11; просмотров: 1272;
