Математический маятник
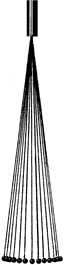 Рис. 3.1
Рис. 3.1
|
Математическим маятником называется материальная точка, подвешенная на невесомой нити или невесомом стержне, которая совершает колебания в вертикальной плоскости под действием силы тяжести.
Металлический шарик, подвешенный на нити, является вполне приемлемой моделью математического маятника.
Попробуем вычислить период малых колебаний математического маятника, то есть таких колебаний, при которых нить отклоняется от вертикали не более чем на 5° (рис. 3.1).
Рассмотрим силы, действующие на шарик массой т, совершающий колебания на нити длиной l. Пусть в данный момент нить составляет с вертикалью угол a, а скорость шарика равна υ (рис. 3.2). На шарик действуют две силы: сила тяжести 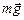 и сила натяжения нити
и сила натяжения нити  .
.
Согласно второму закону Ньютона
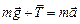 , (1)
, (1)
где 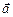 – ускорение шарика.
– ускорение шарика.
Поскольку шарик движется по окружности, то ускорение можно представить в виде векторной суммы двух составляющих векторов:
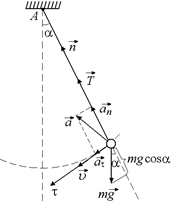 Рис. 3.2
Рис. 3.2
|
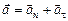 ,
,
где 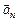 – нормальное ускорение, направленное к центру окружности – точке А, а
– нормальное ускорение, направленное к центру окружности – точке А, а 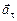 – касательное ускорение (его еще называют тангенциальным), направленное по касательной к окружности.
– касательное ускорение (его еще называют тангенциальным), направленное по касательной к окружности.
Как известно из курса механики,  . Запишем теперь второй закон Ньютона в проекции на ось
. Запишем теперь второй закон Ньютона в проекции на ось 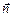 (рис. 3.2), получим
(рис. 3.2), получим
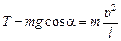 .
.
Теперь на минуту остановимся и подумаем: чем можно пренебречь и что можно упростить, если ограничиться случаем малых колебаний, то есть колебаний, происходящих с очень небольшой скоростью вблизи положения равновесия?
Читатель: Если, как Вы говорите, скорость υ мала, то квадрат скорости υ2, наверное, пренебрежимо мал, то есть им можно пренебречь. Тогда 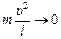 .
.
Автор: А значит, можно считать, что 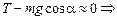
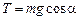 ! Вспомним, что при малых a sina » a. В этом легко убедиться с помощью рис. 3.3: по определению синус угла a равен отрезку АВ – ординате конца единичного подвижного радиуса ОВ, а угол a, выраженный в радианах, численно равен длине дуги А¢В.
! Вспомним, что при малых a sina » a. В этом легко убедиться с помощью рис. 3.3: по определению синус угла a равен отрезку АВ – ординате конца единичного подвижного радиуса ОВ, а угол a, выраженный в радианах, численно равен длине дуги А¢В.
 Рис. 3.3
Рис. 3.3
| Если угол a очень мал, то дуга А¢В и отрезок АВ практически сливаются воедино: А¢В » АВ. Теперь заметим еще одно обстоятельство: при очень малых углах можно считать cosa » 1.
Читатель: Это не очень понятно.
Автор: Воспользуемся основным тригонометрическим тождеством:
cos2a + sin2a = 1,
 . .
|
Добавим под корнем величину a4/4. Она так мала по сравнению с a, что беспокоится не о чем! Получим
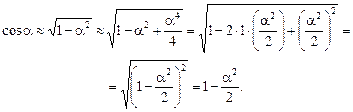
Запомним приближенную формулу:
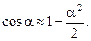 (3.1)
(3.1)
Ясно, что при малых a величиной a2/2 можно пренебречь, и поэтому cosa » 1.
Итак, подытожим наши упрощения и приближения:
1) Т » mgcosa;
2) sina » a;
3) cosa » 1.
Читатель: А с учетом третьего приближения можно упростить и первое: Т » mgcosa » mg×1 = mg.
Автор: Совершенно верно! А теперь вспомним, что при малых углах a окружность мало отличается от прямой, и заменим рис. 3.2 на упрощенный рис. 3.4.
Запишем второй закон Ньютона в проекции на ось х:
–Тsina = тах, (2)
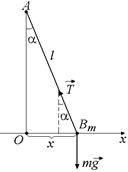 Рис. 3.4
Рис. 3.4
|
где ах – проекция ускорения на ось х. Поскольку Т » mg, а из DАОВ 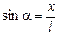 , где х – координата шарика, то из равенства (2) получим
, где х – координата шарика, то из равенства (2) получим
–  ,
,
тогда
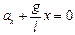 . (3.2)
. (3.2)
А учитывая, что ах = х²(t), получим
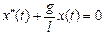 . (3.3)
. (3.3)
Сравним уравнение (3.3) с уже решенным нами уравнением (1.3):
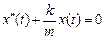 .
.
Разница только в коэффициенте перед х(t): было 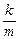 , а стало
, а стало  . Если ввести обозначение
. Если ввести обозначение 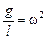 , то наше уравнение примет вид
, то наше уравнение примет вид
 .
.
Его решением, как мы уже выяснили в § 1, является функция 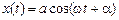 , где а – амплитуда, а a – начальная фаза.
, где а – амплитуда, а a – начальная фаза.
Итак, мы нашли циклическую частоту колебаний математического маятника
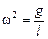 Þ
Þ
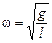 . (3.4)
. (3.4)
Тогда период колебаний составит
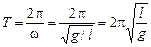 .
.
Запомним: период колебаний математического маятника равен
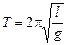 . (3.5)
. (3.5)
Заметим, что период колебаний не зависит от массы шарика!
Из формулы (3.5) нетрудно получить формулу для частоты колебаний
 .
.
Запомним:
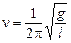 . (3.6)
. (3.6)
СТОП! Решите самостоятельно: А1–А3, В1, С1, С2.
Задача 3.1. Как относятся длины двух математических маятников, если за одно и то же время один из них совершает п1 = 10 колебаний, а второй п2 = 30 колебаний?
| п1 = 10 п2 = 30 | Решение. Пусть оба маятника колеблются время t. Тогда
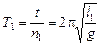 , (1) , (1)
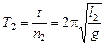 . (2) . (2)
|
| l1/l2 = ? | |
Разделим (1) на (2), получим
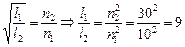 .
.
Ответ: 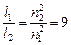 .
.
СТОП! Решите самостоятельно: А4, В2–В5, В7.
Задача 3.2. Математический маятник длиной l = 1 м совершает колебания амплитудой а = 0,02 м. Найти проекции ускорения на ось х в крайних положениях и положении равновесия (см. рис. 3.4). Считать g = 10 м/с2.
| l = 1 м х1 = –0,02 м х2 = 0,02 м х3 = 0 | Решение. Воспользуемся уравнением (3.2):
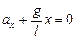 Þ Þ 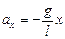 ,
тогда ,
тогда
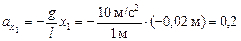 м/с2; м/с2;
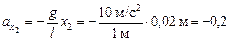 м/с2; м/с2;
|
 = ? = ? 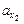 = ? = ?
 = ? = ?
| |
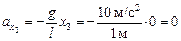 .
.
Ответ: 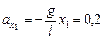 м/с2;
м/с2; 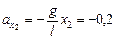 м/с2;
м/с2;
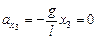 .
.
СТОП! Решите самостоятельно: А5, А6, В6.
Дата добавления: 2016-04-11; просмотров: 3141;
