ДВИЖЕНИЯ С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА
ИЗУЧЕНИЕ ЗАКОНОМЕРНОСТЕЙ ВРАЩАТЕЛЬНОГО
Поскольку любое движение тела можно представить как сумму двух движений:
поступательного со скоростью движения центра масс и вращения вокруг мгновенной оси, проходящей через центр масс, то важность изучения вращательного движения важна.
Рассмотрим движение абсолютно твердого тела вокруг неподвижной оси. Точки тела, лежащие на разных расстояниях от оси вращения, обладают разными скоростями, так как за одно время обходят окружности разной длины. Вместе с тем в заданный промежуток времени все точки поворачиваются на один и тот же угол. Поэтому движение удобно описывать с помощью угловых величин. Угловой скоростью называется вектор 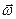 , численно равный первой производной от угла поворота по времени
, численно равный первой производной от угла поворота по времени 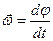 и направленный вдоль оси вращения так, что из его конца видно вращение, происходящее против часовой стрелки. Линейная и угловая скорости связанны соответственно соотношением
и направленный вдоль оси вращения так, что из его конца видно вращение, происходящее против часовой стрелки. Линейная и угловая скорости связанны соответственно соотношением 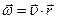 , где
, где 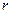 - расстояние точки, имеющей скорость
- расстояние точки, имеющей скорость 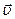 от оси вращения. Для характеристики изменения величины угловой скорости будет введено понятие углового ускорения. Им называется вектор
от оси вращения. Для характеристики изменения величины угловой скорости будет введено понятие углового ускорения. Им называется вектор  , равный по величине первой производной по времени от угловой скорости
, равный по величине первой производной по времени от угловой скорости 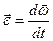 и направленный вдоль оси вращения. Если
и направленный вдоль оси вращения. Если 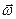 увеличивается (движение ускоренное),
увеличивается (движение ускоренное),  и
и 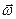 направлены в одну сторону, если движение замедленное (
направлены в одну сторону, если движение замедленное ( 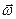 уменьшается) – в противоположную. Линейное ускорение
уменьшается) – в противоположную. Линейное ускорение 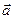 и угловое ускорение
и угловое ускорение  связанны соотношением
связанны соотношением 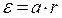 , где
, где 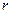 - расстояние точки, имеющей ускорение
- расстояние точки, имеющей ускорение 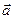 от оси вращения.
от оси вращения.
При действии на тело силы ее вращающее действие определяется не только величиной, но и расстоянием точки приложения силы от оси вращения. С этим связанна необходимость введения нового вектора – момента силы 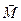 . Поясним это.
. Поясним это.
Пусть тело вращается под действием силы 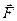 вокруг оси OO’ (рис. 1). Разложим эту силу на две составляющие: параллельную оси вращения
вокруг оси OO’ (рис. 1). Разложим эту силу на две составляющие: параллельную оси вращения 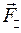 , и перпендикулярную оси вращения
, и перпендикулярную оси вращения  .
.
Компонента силы 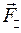 не оказывают динамического действия на тело, т.е. не изменяют скорости его вращения, а лишь деформируют закрепленную ось вращения ОО'. Рассчитаем динамический эффект перпендикулярной компоненты силы. Для этого рассмотрим движение материальной точки
не оказывают динамического действия на тело, т.е. не изменяют скорости его вращения, а лишь деформируют закрепленную ось вращения ОО'. Рассчитаем динамический эффект перпендикулярной компоненты силы. Для этого рассмотрим движение материальной точки
Вращающее действие 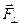 , а, следовательно, и
, а, следовательно, и 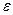 будет тем больше, чем больше величина
будет тем больше, чем больше величина 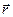 . Поэтому естественно вращающее действие охарактеризовать произведением
. Поэтому естественно вращающее действие охарактеризовать произведением 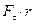 . Заменим ее значением из (1)
. Заменим ее значением из (1) 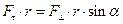 . Но
. Но 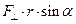 - это величина векторного произведения
- это величина векторного произведения  . И эта же величина характеризует вращательное действие силы
. И эта же величина характеризует вращательное действие силы 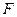 . Таким образом, естественно ввести вектор
. Таким образом, естественно ввести вектор 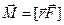 в качестве характеристики вращательного движения силы
в качестве характеристики вращательного движения силы 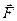 . Этот вектор называется моментом силы
. Этот вектор называется моментом силы 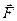 относительно неподвижной оси, как явствует из определения он направлен вдоль оси вращения.
относительно неподвижной оси, как явствует из определения он направлен вдоль оси вращения.
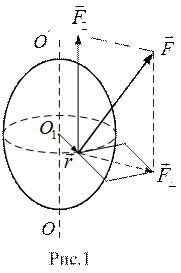
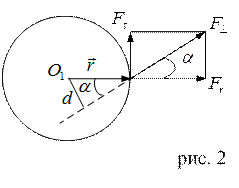
Так, моментом силы 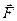 относительно неподвижной оси вращения OO' называется величина, равная векторному произведению составляющей силы
относительно неподвижной оси вращения OO' называется величина, равная векторному произведению составляющей силы 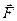 , лежащей в плоскости перпендикулярной оси на лежащий в той же плоскости радиус- вектор, соединяющий точку пересечения оси с точкой приложения силы.
, лежащей в плоскости перпендикулярной оси на лежащий в той же плоскости радиус- вектор, соединяющий точку пересечения оси с точкой приложения силы.
Из рис. 2 видно, что 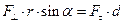 , где
, где 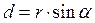 .
.  называется плечом силы
называется плечом силы 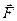 , то есть плечо – это перпендикуляр, опущенный из точки О на направление действия силы.
, то есть плечо – это перпендикуляр, опущенный из точки О на направление действия силы.
Если на тело действует несколько сил, то оно будет находиться в равновесии при условии, что алгебраическая сумма моментов всех сил относительно оси вращения равна нулю.
В динамике поступательного движения инертность тела полностью характеризуется его массой. При вращательном движении инертность тела определяется моментом инерции 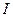 , который зависит не только от массы тела, но и от ее распределения относительно оси вращения.
, который зависит не только от массы тела, но и от ее распределения относительно оси вращения.
Для вращающейся материальной точки момент инерции определяется выражением:
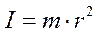 (3)
(3)
где 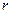 - расстояние точки до оси вращения.
- расстояние точки до оси вращения.
Для системы, состоящей из 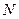 материальных точек:
материальных точек:
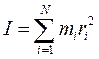 (4)
(4)
где 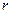 - расстояние материальной точки до оси вращения.
- расстояние материальной точки до оси вращения.
Для сплошного тела сумма переходит в интеграл, и момент инерции определяется по формуле:
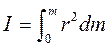 (5)
(5)
Момент силы 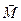 , действует на тело, момент инерции
, действует на тело, момент инерции 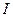 и его угловое ускорение связанны соотношением:
и его угловое ускорение связанны соотношением:
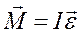 , (6)
, (6)
основной закон вращательного движения.
Из соотношения (5) ясно, что одно и то же тело может иметь бесконечно много моментов инерции и соответственно тело может иметь различную инертность в зависимости от выбранной оси вращения.
Просто вычисляется момент инерции интегрированием (соотношением (5)) для тел правильной геометрической формы, когда ось вращения проходит через центр масс.
Ниже даны моменты инерции двух тел правильной геометрической формы, знание которых необходимо при выполнении данной работы.
1. Момент инерции сплошного цилиндра (или диска) относительно оси 

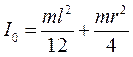
2. Момент инерции тонкого цилиндрического стержня длины относительно оси  :
:

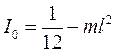
Момент инерции тела относительно оси, не проходящей через центр масс, определяется по теореме Штейнера: момент инерции тела 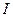 относительно произвольной оси вращения равен сумме момента инерции
относительно произвольной оси вращения равен сумме момента инерции 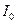 относительно параллельной оси, проходящей через центр масс тела, и величины
относительно параллельной оси, проходящей через центр масс тела, и величины 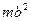 ; где
; где 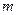 - масса тела, а
- масса тела, а 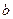 - расстояние от центра масс тела, до произвольной оси вращения:
- расстояние от центра масс тела, до произвольной оси вращения:
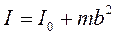 (7)
(7)
Проверить закономерности вращательного движения и теорему Штейнера предлагается на маятнике Обербека.
Описание установки
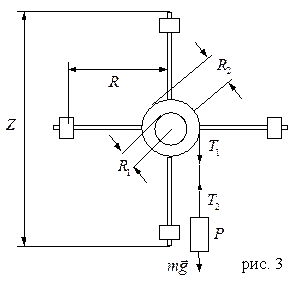 Маятник Обербека состоит из четырех тонких стержней, укрепленных на горизонтальной оси под прямым углом друг к другу.
Маятник Обербека состоит из четырех тонких стержней, укрепленных на горизонтальной оси под прямым углом друг к другу.
На эту же ось насажены два шкива радиусов 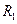 и
и 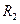 . Вся система свободно вращается вокруг горизонтальной оси. Изменение момента инерции системы осуществляется перемещением цилиндрических грузов
. Вся система свободно вращается вокруг горизонтальной оси. Изменение момента инерции системы осуществляется перемещением цилиндрических грузов 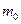 вдоль спиц.
вдоль спиц.
Момент сил определяется силой натяжения нити  . Нить навивается на 1 из шкивов.
. Нить навивается на 1 из шкивов.
Сила натяжения нити  направлена по касательной к поверхности шкива, поэтому вращающий момент силы равен:
направлена по касательной к поверхности шкива, поэтому вращающий момент силы равен:
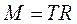 (8)
(8)
Запишем второй закон Ньютона для груза 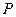 , имеющего массу
, имеющего массу 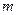 :
:
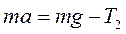 , (9)
, (9)
где 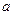 - ускорение несвободного падения груза. Так как сила натяжения
- ускорение несвободного падения груза. Так как сила натяжения  , груз движется равноускоренно. Начальная скорость его равна нулю. Итак, можно подсчитать путь
, груз движется равноускоренно. Начальная скорость его равна нулю. Итак, можно подсчитать путь 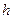 , пройденный в этом движении телом
, пройденный в этом движении телом 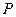 за время
за время  ;
; 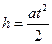 , откуда:
, откуда:
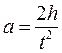 (10)
(10)
Используя соотношения (9) и (10) ( 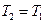 ), момент силы
), момент силы 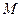 (формула 7), запишем в виде:
(формула 7), запишем в виде:
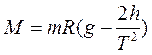 (11)
(11)
Ясно, что касательное ускорение точек поверхности шкива имеет то же ускорение 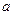 , как и тело
, как и тело 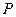 .
.
Из соотношения (1) и (10) имеем:

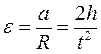 (12)
(12)
Формулы (11) и (12) позволяют проверить основной закон динамики вращательного движения:
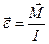
Порядок выполнения работы
Задание 1
1. Измерить диаметры малого и большого шкивов 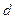 и
и 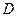 с помощью штангенциркуля, результаты измерений занести в таблицу.
с помощью штангенциркуля, результаты измерений занести в таблицу.
2. Закрепить на концах стержней цилиндрические грузы так, чтобы маятник находился в состоянии безразличного равновесия.
3. Намотать нить на шкив большого и малого диаметра (по указанию преподавателя). Подвесить груз и измерить его высоту над полом.
4. Измерить секундомером время падения груза. Повторить опыт не менее трех раз. По формуле (12) определить 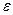 , а затем найти
, а затем найти 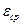 .
.
5. Повторить опыт, описанный в пункте 4, для пяти-шести грузов с различными массами.
6. Результаты эксперимента предоставить в виде графика, по оси ординат отложить угловое ускорение маятника 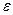 , а по оси абсцисс – величины момента сил
, а по оси абсцисс – величины момента сил 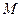 , вычисленные по формуле (11).
, вычисленные по формуле (11).
7. Определить по графику 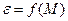 момент инерции системы
момент инерции системы  , который будет равен 1/tgα, где α угол наклона функции
, который будет равен 1/tgα, где α угол наклона функции 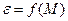 к оси абсцисс (M).
к оси абсцисс (M).
8. Повторить опыты, описанные в пунктах 3,4,5, при новом значении момента инерции системы, переместив цилиндрические грузы на середину стержней. Построить график 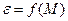 и определить, как указанно в п. 7 новое значение момента инерции
и определить, как указанно в п. 7 новое значение момента инерции 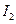 .
.
9. Убедиться в справедливости соотношения 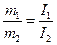 при
при 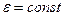 , для этого по двум полученным графикам для одинаковых значений
, для этого по двум полученным графикам для одинаковых значений  определить
определить  и
и  .
.
10. Убедиться в справедливости соотношения 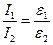 при
при 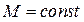 , для этого по двум полученным графикам для одинаковых значений
, для этого по двум полученным графикам для одинаковых значений 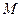 определить
определить 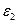 и
и 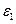 .
.
Находятся ли результаты эксперимента в согласии с формулой (6)? Укажите возможные причины ошибок эксперимента.
Задание 2
1. Убедиться в справедливости теоремы Штейнера, сравнив полученное из опытов (п. 7 задания 1) значения момента инерции с теоретическим значением:
 , (13)
, (13)
где 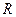 - расстояние центров цилиндрических грузов массой
- расстояние центров цилиндрических грузов массой 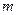 от оси вращения,
от оси вращения,  - длина цилиндрических грузов,
- длина цилиндрических грузов, 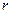 - их диаметр,
- их диаметр, 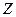 - длина стержней (обязательно посмотрите рис. 3),
- длина стержней (обязательно посмотрите рис. 3),  их масса,
их масса, 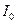 - момент инерции дисков. Масса грузов указана на установке, а так же масса и длина стержней.
- момент инерции дисков. Масса грузов указана на установке, а так же масса и длина стержней.
2. Вычислить относительную погрешность определения момента инерции 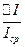 .
.
3. Вычислить абсолютную погрешность  .
.
4. Записать окончательный результат в виде:
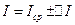
Дата добавления: 2016-03-15; просмотров: 1958;
