Принцип эквивалентности

Задача 3.4.Шарик массы т подвешен внутри пустой цистерны на невесомой нити длиной l. В начальный момент t = 0 цистерна начинает двигаться в горизонтальном направлении с постоянным ускорением а (рис. 3.9). Найти период колебаний шарика.

т l a t = 0	Решение. Начнем с того, что сформулируем один важный физический закон – принцип эквивалентности. Чтобы сформулировать принцип эквивалентности, рассмотрим следующий мыс­ленный эксперимент.	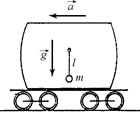Рис. 3.9
Т = ?

Пусть за­крытая лаборатория, например кабина лифта, движется с постоянным ускорением а относительно какой-либо инерциальной системы отсчета в области пространства, где отсутствует поле тяготения. Тогда все свободные тела в лифте, которые относительно инерциальной системы не имеют ускорения, будут относительно лифта иметь одина­ковое ускорение – 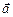. Находящийся в закрытом лифте на­блюдатель, который не имеет возможности «выглянуть наружу», по поведению этих тел не сможет решить, движет­ся ли лифт с ускорением – 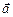или он покоится в однородном поле тяжести, напряженность которого 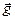равна – 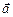. В са­мом деле, при действии такого поля тяжести все свободные тела в покоящемся лифте будут двигаться с одинаковым ускорением .

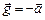Такаяэквивалентность поля тяжести и ускоренного движения системы отсчета справедлива для любых меха­нических явлений: все механические явления в движущемся с ускорением лифте происходят точно так же, как и в не­подвижном лифте, но находящемся в поле тяжести. Сфор­мулировав этот принцип, Эйнштейн распространил его, так же как и принцип относительности, не только на меха­нические явления, но и на все физические явления вообще.

Рис. 3.10

Применение принципа эквивалентности позволяет уп­ростить рассмотрение многих физических явлений, а нашу задачу вообще превращает в тривиальную. Вместо того чтобы рассматривать ускоренно движущуюся цистерну, будем считать, что она неподвижна, но на все тела в ней действует дополнительное гравитационное поле с напряженностью (рис. 3.10,а). Это поле, складываясь с истинным полем тя­жести Земли, дает эффективное поле тяжести,напряженность которого 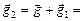.Вектор отклонен от истинной верти­кали на угол a₀, тангенс которого определяется соотношением

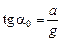. (1)

Величина напряженности эффектив­ного поля тяжести находится по тео­реме Пифагора

. (2)

Ясно, что в положении равновесия нить маятника направ­лена вдоль вектора . В начальный момент, когда цистерна начинает двигаться с ускорением 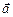, шарик неподвижен, а нить вертикальна, т.е. маятник отклонен от нового положения равновесия на угол a₀, влево (рис. 3.10,б). По­этому маятник в пустой цистерне будет совершать отно­сительно нового положения равновесия колебания с уг­ловой амплитудой a₀. Если ускорение цистерны 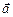мало по сравнению с ускорением свободного падения 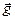,то ампли­туда колебаний мала и колебания будут гармоническими.

Тогда период можно вычислить по формуле (3.5):

.

Ответ: .

Читатель: В этой задаче Вы называете 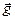напряженностью гравитационного поля, но ведь 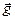– это ускорение свободного падения.

Автор: Да, но, так сказать, по совместительству. Ведь 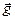– это величина, численно равная силе тяжести, действующей в данной точке поля на единичную массу: 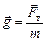. Поэтому она характеризует «силовые возможности» данного поля и (по аналогии с напряженностью электрического поля) называется напряженностью гравитационного поля.

СТОП! Решите самостоятельно: В12, В13, С5, С6.

Маятник в горах

Задача 3.5. На сколько отстанут маятниковые часы в горах на высоте h над поверхностью Земли за время t? Радиус Земли равен R.

h R t	Решение. Отставание маятниковых часов в горах связано с тем, что период колебаний маятника Т = 2p 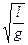зависит от ускорения свободного падения. При подъеме
Dt = ?

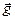уменьшается. В самом деле, согласно закону всемирного тяготения на тело массой т на поверхности Земли действует сила тяжести, равная

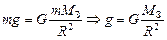, (1)

а на высоте h

, (2)

Разделив (2) на (1), получим .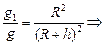

. (3.11)

Поскольку с высотой g₁ уменьшается, то Т увеличивается, значит, период колебаний Т₁ на высоте h будет больше Т: T₁> T. Тогда за каждый период Т₁ часы в горах будут отставать на время (Т₁ – Т).

За время t часы совершают N₁ = t/Т₁ колебаний, поэтому общее отставание составит

Dt = N₁(T₁ – Т) =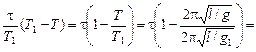

.

Итак, мы получили ответ: часы отстанут на время

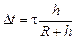. (3.12)

СТОП! Решите самостоятельно: В14, С8–С10.