Задачи средней трудности. В1. Два одинаковых полых шара с отверстиями наполнены один водой, другой песком и подвешены на нитях одинаковой длины

В1. Два одинаковых полых шара с отверстиями наполнены один водой, другой песком и подвешены на нитях одинаковой длины. Шары отклонены на одинаковые углы. Будут ли у них одинаковыми периоды колебаний? Одинаково ли долго будут они колебаться?

В2.Шарик подвешен на длинной нити. Первый раз его поднимают по вертикали до точки подвеса, второй раз отклоняют на небольшой угол. В каком из этих слу­чаев шарик быстрее возвратится к начальному положе­нию, если его отпустить? t₁/t₂ = ?

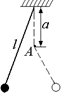Рис. 3.11

В3.Маятник представляет собой упругий шарик, прикрепленный к концу нити, имеющей длину l. При коле­баниях шарик сталкивается с упругой массивной стенкой в моменты, когда нить занимает вертикальное положение. Найти период Т колебаний маятника. Длительностью столкновения пре­небречь.

В4. Математический маятник дли­ной l совершает колебания вблизи вер­тикальной стенки. Под точкой под­веса маятника, на расстоянии a = l/2от нее в стенку вбит гвоздь (рис. 3.11). Найти период Т колебаний маятника.

В5. Масса Луны в 81 раз меньше массы Земли, а радиус Земли в 3,7 раза больше радиуса Луны. Как изменится период колебании маятника при перенесении его с Земли на Луну?

В6.Математический маятник длиной 1,0 м колеблется с амплитудой 1,0 см. За какое время он пройдет путь в 1,0 см, если начнет движение из положения равновесия? За какое время он пройдет: а) первую половину этого пути; б) вторую половину этого пути?

В7. Один из маятников за некоторое время совершил п₁ = 10 колебаний. Другой за то же время совершил п₂ = 6 колебаний. Разность длин маятников Dl = 16 см. Найти длины маятников l₁и l₂.

В8.Найти потенциальную энергию U математического маятника массы т = 200 г в положении, соответствующем углу отклонения нити от вертикали a = 10°, если частота ко­лебаний маятника n = 0,5 с^–1. Считать потенциальную энер­гию маятника в положении равновесия равной нулю.

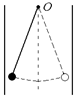Рис. 3.12 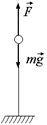  Рис. 3.13

В9. Металлический шарик на длинной нити помещен между обкладками конденса­тора, как показано на рис. 3.12. Как изменится характер колебаний этого маятника, если шарик и пластины конденсатора зарядить? Маятник совершал колебания в плоскости, перпендикулярной к пластинам.

В10. Шарик массы т = 0,10 г закреплен на нити, длина которой l велика по сравнению с размерами шарика. Ша­рику сообщают заряд q = 10 нКл и помещают в однородное электрическое поле с напряженностью Е, направленной вверх. С каким периодом будет колебаться шарик, если сила, действующая на него со стороны электрического поля, больше силы тяжести (F > mg)?Какой должна быть напряженность поля Е, чтобы шарик колебался с периодом 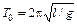(рис. 3.13)?

В11. Шарик массой т, подвешенный на нити, соверша­ет колебания. Как изменится частота колебаний, если ша­рику сообщить положительный заряд q и поместить его в однородное электрическое поле напряженностью Е, сило­вые линии которого направлены вертикально вниз?

В12. В кабине лифта, находящегося на верхнем этаже небоскреба, раскачивается подвешенный на нити шарик. Нить привязана к гвоздю, вбитому в стену кабины. Трос лифта обрывается, и лифт начинает падать. Опишите движение шарика относительно лиф­та на протяжении всего движения лифта. Учтите при этом, что сила сопротивления воздуха быстро растет с увеличением ско­рости.

В13. Космический корабль при включении двигателей дви­жется с некоторым ускорением. Каким образом, используя ма­тематический маятник, подвешенный в кабине корабля, можно определить ускорение корабля?

В14. Определить, на сколько отстанут маятниковые часы за сутки, если их поднять на высоту 5,0 км над поверхностью Земли.

В15.В некоторых старинных часах, предназначенных для работы на открытом воздухе, маятник изготовлялся в виде длинной трубки, заканчивающейся сосудом с ртутью. С какой целью исполь­зовалась такая конструкция маятника?

B16. При температуре q₁ = 20 °С период колебаний маят­ника Т₁ = 2,0 с. Как изменится период колебаний, если тем­пература возрастет до q₂ = = 30 °С? Коэффициент линейного расширения материала маятника a = = 1,85×10^–5 К^–1.

Задачи трудные

С1. Доказать, что период колебаний математического маятника увеличивается с увеличением максимального угла отклонения от положения равновесия.

С2. Груз на длинной нити может совершать колебания в вертикальной плоскости, отклоняясь на угол a от вер­тикали (математический маятник). Этот же груз может вращаться по окружности так, что описывает конус (коничес­кий маятник). В каком случае натяжение нити, отклонен­ной на угол a от вертикали, будет больше?

С3. Положительно заряженный шарик массой т = 30 г (математический маятник) совершает гармонические колеба­ния над положительно заряженной бесконечной горизонталь­ной плоскостью. При этом сила электрического взаимодейст­вия шарика с плоскостью F = 0,10 Н, а период его колебаний Т₁= 2,0 с. Затем шарик перезарядили так, что его заряд стал отрицательным, но по модулю равным первоначальному. Оп­ределите период гармонических колебаний шарика в новом состоянии. Ускорение свободного падения g = 10 м/с².

С4.Математический маятник (длина нити l) помещен в однородное электрическое поле напряженностью Е. Грузу маятника сообщен заряд q. Опре­делите заряд, при котором периоды колебаний маятника в поле и в отсутствие его будут одинаковы. Масса груза равна т.

С5. С каким ускорением а и в каком направлении должна двигаться кабина лифта, чтобы находящийся в ней секундный маятник за время t = = 2 мин 30 с совершил п = 100 колебаний?

С6.В неподвижном лифте висит маятник, период колебаний которого Т = 1,0 с. С каким ускорением движется лифт, если период колебаний этого маятника стал равным Т₁= 1,1 с? В каком направлении движется лифт?

С7. На какую часть длины надо уменьшить длину математического маятника, чтобы период колебаний маятника на высоте 10 км был равен периоду его колебаний на поверхности Земли?

С8.Как-то, гуляя, я невзначай забрался в горы. Мне, конечно, захотелось узнать, на какой я высоте. В моей сумке слу­чайно оказались маятниковые часы. Держа их в правой руке, я начал сравнивать их ход с ходом электронных часов на левом запястье. Ровно через час я обнаружил, что маятниковые часы отстали на пять секунд, и сразу понял, на какой высоте нахожусь. Попробуйте и вы узнать эту высоту. Маятник моих часов сделан из такого сплава, что длина его от температуры не зависит, а мои электронные часы, как известно, самые точные в мире. Радиус Земли R = 6400 км.

С9. В ракете, поднимающейся вверх с ускорением а, находится математический маятник. Объясните характер колебаний маятника в движущейся ракете и определите, на какой высоте период его колебаний станет таким же, как в ракете, стоящей на Земле.

С10. Часы с маятником на поверхности земли идут точно. В каком случае эти часы больше отстанут за сутки: если их поднять на высоту 200 м или же опустить в шахту на глубину 200 м? (Землю считать однородным шаром.)

С11.На сколько часы будут уходить вперед за сутки при t₀ = 0 °С, если они выверены при t = 20 °С, и материал, из которого сделан маятник, имеет коэффициент линейного расширения a = 0,000012 К^–1?

С12. При t₀ = 0 °С часы спешат в сутки на t = 20 с. При какой температуре часы будут идти точно? Коэффициент линейного расширения материала маятника a = 1,9×10^–5 К^–1.