Задачи средней трудности. В1. Как раскачать стрелку заряженного электрометра, не имея заряженного тела?
В1. Как раскачать стрелку заряженного электрометра, не имея заряженного тела? Проверьте на опыте и объясните явление.
В2. На некоторых участках дороги встречаются расположенные на приблизительно одинаковых расстояниях выбоины (это обычно отмечается соответствующим дорожным знаком). Водитель вел автомобиль по такому участку один раз порожним, а другой раз нагруженным. Сравнить скорости движения машины, при которых наступит резонансное раскачивание на рессорах.
В3. За счет какой энергии поддерживаются незатухающие колебания при качании на качелях? Можно ли назвать эту систему автоколебательной?
В4. Мальчик несет на коромысле ведра с водой, период собственных колебаний которых 1,6 с. При какой скорости движения вода начнет особенно сильно выплескиваться, если длина шага мальчика 60 см.
В5.При какой максимальной скорости движения поезда может возникнуть резонанс вертикальных колебаний вагона вследствие периодических ударов колёс на стыках рельсов, если длина рельса между стыками 25 м, а период собственных вертикальных колебаний вагона примерно равен 1,25 с?
В6. За счет какой энергии поддерживаются незатухающие колебания системы (см. рис. 4.4)?
Задача трудная
С1. Маленький шарик подвешен на нити длиной 1,0 м к потолку вагона. При какой скорости вагона шарик будет особенно сильно колебаться под действием ударов колес о стыки рельсов? Длина рельса 12,5 м.
Нестандартные задачи
На механические колебания
Основной вопрос, который возникает при рассмотрении той или иной колебательной системы – это определение периода колебаний. Мы рассмотрим два основных способа вычисления периода: динамический метод и метод полной энергии.
Динамический метод
Суть метода состоит в том, чтобы определить величину квазиупругой силы, возникающей в системе при отклонении колеблющегося тела от положения равновесия на малое смещение х: Fx = – kx. Самое главное – определить коэффициент k. Как только он найден, задача практически решена:
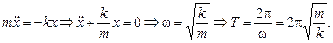
Покажем, как «работает» этот метод на конкретных примерах.
Задача 5.1.В жидкости плотностью rж плавает цилиндр высотой h. Если цилиндр глубже погрузить в жидкость или, напротив, немного вытащить из жидкости, то после того как его отпустят, цилиндр начинает колебаться. Плотность материала, из которого сделан цилиндр, rм. Определите частоту колебаний цилиндра.
| rж rм h | Решение. Условие плавания тела: сила Архимеда равна силе тяжести (рис. 5.1): Fвыт = Fтили rжSх0g = rмShg, где S – площадь поперечного сечения цилиндра, х0 – глубина его погружения. |
| n = ? | |
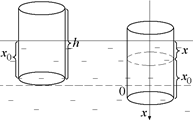 Рис. 5.1
Рис. 5.1
|
Если увеличить глубину погружения цилиндра, то сила тяжести не будет компенсировать выталкивающую силу и второй закон Ньютона для цилиндра (в проекции на направление оси х, вдоль которой совершаются колебания) будет иметь вид
тах = –rжSgx, (1)
Таким образом, мы определили значение квазиупругой силы
Fx = –kx = –(rжSg)x.
Поскольку масса цилиндра т = rмV = rмSh, получим:

 rмShах = –rжSgх Þ
rмShах = –rжSgх Þ 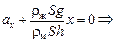
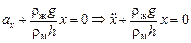 . (2)
. (2)
Сравнивая уравнение (2) с известным нам уравнением 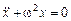 , получаем, что
, получаем, что
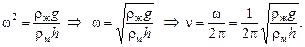
Задача решена.
Ответ: 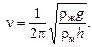
СТОП! Решите самостоятельно: В1, В2, С1, С2, D1.
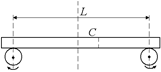 Рис. 5.2
Рис. 5.2
|
Задача 5.2.На два быстро вращающихся одинаковых валика положили горизонтально доску с массой т (рис. 5.2). Расстояние между осями валиков равно L, коэффициент трения между доской и валиками равен m. Какое движение будет совершать доска? Как изменится ответ, если оба валика изменят направление вращения?
| т L m | Решение. Очевидно, если центр доски расположен нa равных расстояниях от обоих валиков, то доска будет оставаться в равновесии. В любом другом случае доска придет в движение. Поскольку в условии говорится о быстром вращении валиков, между ними и доской происходит |
| Т = ? | |
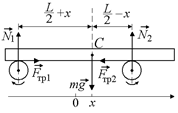 Рис. 5.3
Рис. 5.3
|
проскальзывание, и сила трения скольжения, действующая на доску со стороны каждого из валиков, направлена внутрь (рис. 5.3).
Из второго закона Ньютона и формулы для силы трения скольжения следует, что
maх = Fтр1 – Fтр2 = m(N1 – N2),
где N1 и N2– силы нормальной реакции первого и второго валиков соответственно.
Найдем силы N1 и N2. Для этого запишем второе условие равновесия твердого тела (условие равенства нулю моментов всех сил, действующих на тело относительно любой оси вращения). Это условие выполняется, так как хотя доска движется ускоренно вдоль оси х, но при этом не вращается.
На доску действуют пять сил: 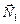 ,
, 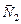 ,
, 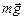 ,
, 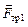 и
и 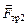 . Запишем их моменты относительно точки С. Напомним, что моментом силы относительно оси вращения называется произведение величины силы на плечо.
. Запишем их моменты относительно точки С. Напомним, что моментом силы относительно оси вращения называется произведение величины силы на плечо.
Плечо – это расстояние от точки приложения силы до направления действия силы.
Момент берется со знаком «плюс», если данная сила вращает тело вокруг данной оси по часовой стрелке, и со знаком «минус», если против.
Отметим, что плечи сил 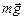 ,
, 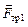 и
и 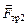 равны нулю, так как направления действия этих сил проходят через точку С (см. рис. 5.3). Плечо силы N1 равно (L/2 + х), а плечо силы N2 равно (L/2 – х). Отсюда
равны нулю, так как направления действия этих сил проходят через точку С (см. рис. 5.3). Плечо силы N1 равно (L/2 + х), а плечо силы N2 равно (L/2 – х). Отсюда
N1(L/2 + х) – N2 (L/2 – х) = 0. (1)
Поскольку в вертикальном направлении ускорение равно нулю, то
N1 + N2 – mg = 0. (2)
Из (2) находим N2 = mg – N1 и подставим в (1):
N1(L/2 + х) – (mg – N1)(L/2 – х) = 0 Þ
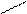
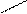
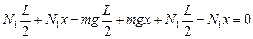 Þ
Þ
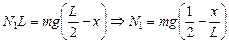 ,
,
тогда
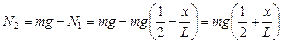 .
.
Теперь запишем второй закон Ньютона в проекции на ось х, подставив в него найденные значения N1 и N2:
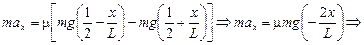
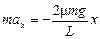 .
.
Мы записали выражение для нашей квазиупругой силы Fx = –kx. Дальше все просто:
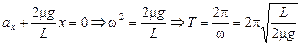 ,
,
т.е. доска будет совершать гармонические колебания с периодом
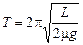 .
.
Читатель: А что будет, если валики будут вращаться в обратную сторону?
Автор: Если каждый валик станет вращаться в обратную сторону, то обе силы трения будут направлены «наружу». Смещение доски от положения равновесия увеличит (за счет перераспределения нагрузки на валики) как paз ту силу трения, которая действует в сторону смещения (и уменьшит силу трения о другой валик). Поэтому вместо возвращающей силы возникает сила, уводящая доску еще дальше от положения равновесия. Равновесие в этом случае неустойчиво, колебаний вокруг него не возникает. Доска будет сброшена с валиков.
СТОП! Решите самостоятельно: С3, D2.
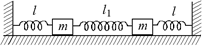 Рис. 5.4
Рис. 5.4
|
Задача 5.3.Два одинаковых груза массой т, скрепленные пружинами, как показано на рис. 5.4, лежат на абсолютно гладком горизонтальном столе. Пружины растянуты с силой F. Грузы смещают в направлении, перпендикулярном длине пружин, на одинаковое малое расстояние х в одну сторону от положения равновесия. Определить период колебаний грузов.
| т l F | Решение. Рассмотрим малое смещение грузов на расстояние х вдоль оси х (рис. 5.5).
Рис. 5.5 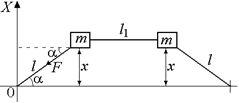
|
| Т = ? | |
Поскольку х мало, можно считать, что величина силы F увеличилась незначительно. В проекции на ось х запишем второй закон Ньютона для левого тела:
max = –Fsina = –F 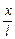 Þ
Þ 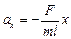 .
.
Следовательно, 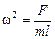 , отсюда
, отсюда 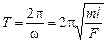 .
.
Ответ: 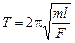 .
.
СТОП! Решите самостоятельно: В3, С4.
Задача 5.4. Определить период малых колебаний полярной молекулы в однородном электрическом поле, напряженность которого Е = 3×104 В/м. Полярную молекулу схематически представить в виде «гантельки» длиной l (l = 1×10–8 см), на концах которой находятся равные точечные массы m (m = 4×10–24 г), несущие заряды +q и –q соответственно (q = 15,7×10–20 Кл).
| Е = 3×104 В/м l = 1×10–8 см m = 4×10–24 г q = 15,7×10–20 Кл | Решение. В силу симметрии молекулы оба атома, составляющие молекулу, будут совершать колебания относительно центра масс системы – точки С (рис. 5.6). Оба атома находятся в совершенно одинаковых условиях, поэтому достаточно рассмотреть движение одного из них.
Пусть нижний атом совершил малое смещение х от положения равновесия и оказался в точке А. Запишем второй закон Ньютона в проекции на оси х и Y:
Х: –Тsina = max, (1)
Y: Tcosa – Eq = 0. (2)
Поскольку х << l, то a ® 0, сosa » 1 и Т » Eq. Из DАОС имеем
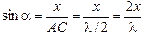 . .
|
| Т = ? | |
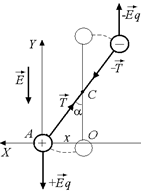 Рис. 5.6
Рис. 5.6
|
Подставляя в (1) значения Т и sina, получим
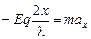 Þ
Þ 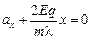 Þ
Þ 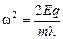 Þ
Þ
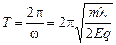 .
.
Подставим численные значения
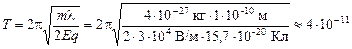 с.
с.
Ответ: 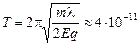 с.
с.
СТОП! Решите самостоятельно: С5, D3–D5.
Задача 5.5. Определить период малых колебаний маленького кубика массой т в сферической чаше радиусом R. Трения нет.
| т R | Решение. Запишем второй закон Ньютона в проекциях на оси Х и Y (рис. 5.7). Как и раньше в таких задачах, движение по окружности при малых углах a можно заменить на движение по прямой – оси Х. Тогда | 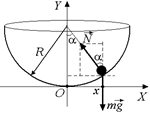 Рис. 5.7
Рис. 5.7
|
| Т = ? | ||
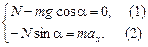
Учтем, что N » mg (так как cosa » 1) и sina 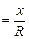 . Подставим значения N и sina в (2) и получим
. Подставим значения N и sina в (2) и получим
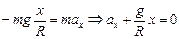 .
.
Следовательно,
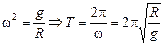 .
.
Заметим, что период получился таким же, как и для математического маятника с длиной l = R.
Ответ: 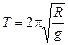 .
.
СТОП! Решите самостоятельно: В4–В6, D6.
Дата добавления: 2016-04-11; просмотров: 2274;
