Задачи очень трудные. D1. Тонкое проволочное кольцо радиуса R имеет элект­рический заряд +Q

D1. Тонкое проволочное кольцо радиуса R имеет элект­рический заряд +Q. Как будет двигаться точечное тело массы т, имеющее заряд –q,если в начальный момент вре­мени оно покоилось в некоторой точке на оси кольца на расстоянии x << R от его центра? Кольцо неподвижно.

D2. Два плоских слоя толщины d каждый равномерно заряжены объемным зарядом с плотностями –r и +r. Частица с отрицательным зарядом –е и массой т подле­тает к положительно заряженному слою со скоростью υ, на­правленной под углом aк поверхности слоя (рис. 5.18). Определить:

а) при какой скорости частица не сможет проникнуть в отрицательно заряженный слой?

б) через сколько времени и на каком расстоянии от точки А частица в этом случае покинет положительно заряженный слой?

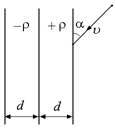
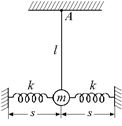
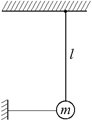
Рис. 5.18 Рис. 5.19 Рис. 5.20

D3. Комбинированный маятник. Рассмотрим маятник, изображенный на рис. 5.19. Легкий стержень длины l подвешен на оси в точке А таким образом, что он может двигаться в плоскости чертежа. К грузу массы т на конце стержня прикреплены одинаковые пружины же­сткости k, расположенные горизонтально в этой же плос­кости. Другие концы пружин закреплены неподвижно. Найти частоту малых собственных колебаний такого маятника в отсутствие трения. Массами стержня и пружин пренебречь.

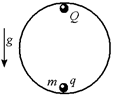Рис. 5.21

D4. Несимметричный маятник.С одной сто­роны к грузу прикреплена гибкая резинка, проявляю­щая упругие свойства только при растяжении (рис. 5.20). Когда маятник расположен вертикально, резинка не натянута. Смещение груза вправо приводит к растяже­нию резинки, которое удовлетворяет закону Гука: F = –kx. При смещении груза влево резинка просто про­висает. Найти период собственных колебаний такого несимметричного маятника.

D5. Найдите частоту малых колебаний математического маятника относительно его нижнего положения равновесия, если непосредственно под равновесным положением шарика на расстоянии h от него закреплен заряд Q. Длина нити l, масса шарика т, заряд q.

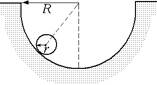Рис. 5.22

D6. Найдите период малых колебаний тела массы т, заряд которо­го q,внутри гладкой сферы радиуса R, если в верхней точке сферы зак­реплен заряд Q (рис. 5.21). Заряды q и Q разных знаков: qQ < 0.

D7. Обруч массы т и радиуса r может катиться без про­скальзывания по внутренней по­верхности цилиндра радиуса R (рис. 5.22). Определить период колебаний обруча, считая угол j малым.

[1] Все численные значения в этой и всех последующих задачах данного параграфа являются абсолютно точными и заданными в СИ.

[2] В задачах этого параграфа, если нет специальных оговорок, считать, что: а) колебательное движение задается уравнением х = х_тcoswt; б) все величины заданы в единицах СИ; в) движение изучается в пределах одного периода; г) все начальные данные – точные.

[3] В задачах этого параграфа, если нет специальных оговорок, считать, что колебательное движение задается уравнением х = х_тcoswt.

[4] Немецкое слово анкер означает якорь.