Метод полной энергии
Пусть имеется некоторая колебательная система. Пусть смещение колеблющегося тела от положения равновесия равно х. Тогда скорость тела в момент времени t: υх = х¢(t).
Допустим, что нам удалось записать выражение для полной механической энергии системы в виде
Е = Ах2 + В(х¢)2. (5.1)
Тогда циклическая частота w такой системы равна
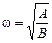 . (5.2)
. (5.2)
Докажем наше утверждение.
Если в системе отсутствует трение, то полная механическая энергия системы остается постоянной: E(t) = const, а значит, производная энергии по времени равна нулю: E¢(t) = 0.
Продифференцируем выражение (5.1) и приравняем его производную к нулю:
Е¢(t) = (Ах2(t) + В(х¢(t)2)¢ = А×2х(t)х¢(t) + В×2×х¢(t)×х¢¢(t) = 0 Þ
2×х¢(t)×(Ах(t) + Вх¢¢(t)) = 0 Þ х¢¢(t) + 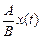 = 0.
= 0.
Мы получили уже хорошо знакомое нам уравнение, решением которого является функция х(t) = acos(wt + a), где 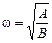 .
.
Наше утверждение доказано.
Попробуем применить формулы (5.1) и (5.2) для решения задач.
Задача 5.6.Плоская Т-образная конструкция из трёх небольших шариков может свободно поворачиваться в вертикальной плоскости вокруг горизонтальной оси О (рис. 5.8) (плоскость рисунка перпендикулярна оси О). Длина каждой спицы L, а масса пренебрежимо мала по сравнению с массой шариков. Определите период малых колебаний конструкции.
| L | 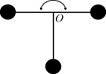 Рис. 5.9 Рис. 5.9 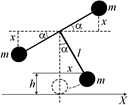
|
| T = ? | |
| Рис. 5.8 |
Решение. Пусть масса каждого шарика равна т, и вся система повернулась на малый угол a. Тогда левый шарик опустился на х вниз, а правый поднялся на х вверх, следовательно, общая потенциальная энергия этих двух шариков не изменилась.
Нижний шарик поднялся вверх на величину h = l(1 – cosa). С учетом того, что при малых a 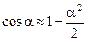 , получим
, получим
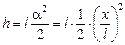 .
.
Значит, если потенциальную энергию в положении равновесия считать равной нулю, то при отклонении системы на малый угол a потенциальная энергия будет равна
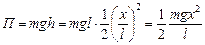 .
.
Скорости у всех трех шариков одинаковы и равны υх = х¢(t). Тогда кинетическая энергия системы равна
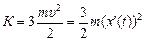 .
.
Находим полную энергию:
Е = П + К = 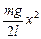 +
+ 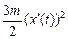 .
.
Сравнивая полученную формулу с (5.1), получим
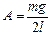 ,
, 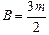 .
.
Тогда
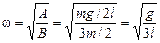 Þ
Þ 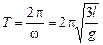 .
.
Ответ: 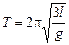 .
.
СТОП! Решите самостоятельно: С6, С7, D7.
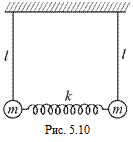 Задача 5.7.Два математических маятника длиной l каждый связаны невесомой пружиной с жесткостью k. На рис. 5.10 показано положение равновесия системы. Маятники отклоняют в плоскости рисунка на одинаковые углы и отпускают. Определите период Т малых колебаний связанных маятников, если: а) маятники отклонены в одну сторону (колебания в одной фазе); б) маятники отклонены в противоположные стороны (колебания в противофазе). Масса каждого шарика равна т.
Задача 5.7.Два математических маятника длиной l каждый связаны невесомой пружиной с жесткостью k. На рис. 5.10 показано положение равновесия системы. Маятники отклоняют в плоскости рисунка на одинаковые углы и отпускают. Определите период Т малых колебаний связанных маятников, если: а) маятники отклонены в одну сторону (колебания в одной фазе); б) маятники отклонены в противоположные стороны (колебания в противофазе). Масса каждого шарика равна т.
| m k l | Решение. а) Пружина не деформируется при колебаниях, так что сила упругости не возникает (связь между маятниками «не работает») (рис. 5.11,а). Поэтому оба маятника колеблются независимо друг от друга с одним и тем же периодом 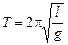 . .
| |
| T = ? | ||
а 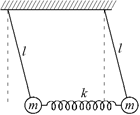
| б 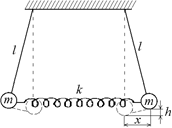
| |
Рис. 5.11
б) Во втором случае (рис. 5.11,б) каждый шар отклонили на расстояние х, следовательно, пружина удлинилась на 2х, и ее потенциальная энергия стала равна
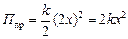 .
.
Каждый шарик поднялся на высоту
h = l(1 – cosa) » 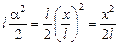 .
.
Потенциальная энергия шариков в поле силы тяжести стала равна
Пт = 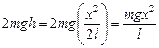 .
.
Кроме того, каждый шарик приобрел скорость υх = х¢, а значит, и кинетическую энергию. Общая кинетическая энергия системы стала равна
К = 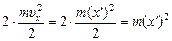 .
.
Находим полную механическую энергию системы
Е = Ппр + Пт + К = 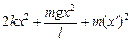 Þ
Þ
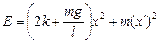 .
.
Следовательно, 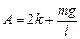 , В = т. Тогда
, В = т. Тогда
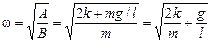 Þ
Þ 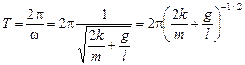 .
.
Ответ: 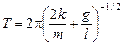 .
.
СТОП! Решите самостоятельно: С8, С9, С10.
Дата добавления: 2016-04-11; просмотров: 2686;
