Движение по наклонной плоскости

Задача 18.5. Маленький шарик массы т и заряда +q находится на вершине наклонной плоскости. Высота наклонной плоскости h, а угол наклона a. Над нижней точкой наклонной плоскости на высоте h закреплен неподвижно заряд +q (рис. 18.5). Шарик соскальзывает с наклонной плоскости без начальной скорости. Найти его скорость у основания плоскости.

+q h a	Решение. Попробуем решить эту задачу с помощью закона сохранения энергии: энергия шарика в верхней точке равна энергии шарика в нижней точке: Едо = Епосле.	Рис. 18.5
υ = ?

Учтем, что

Е_до = П_до + К_до = П_{mg до} + П_{е до} + К_до,

поскольку

П_{mg до} = mgh, П_{е до} = qj_до = 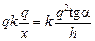, К_до = 0,

где учтено, что х = hctga = 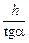, тогда

Е_до = mgh + + 0;

Е_после = П_после + К_после = П_{mg после} + П_{е после} + К_после.

поскольку

П_{mg после} = 0, П_{е после} = qj_после = 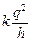, К_после = ,

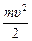тогда

Е_после = 0 + + .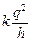

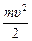Итак, закон сохранения энергии имеет вид

mgh + = + .

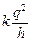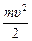Отсюда

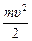= mgh + 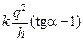Þ .

Ответ: .

СТОП! Решите самостоятельно: В3, С1, С5.

Маятник

Задача 18.6. Маленький шарик массы т и заряда +q подвешен на нити длиной l и может совершать колебания в вертикальной плоскости. На расстоянии 2l по вертикали под точкой подвеса закреплен заряд +q. Шарик отклонили так, что нить приняла горизонтальное положение, и отпустили без начальной скорости (рис. 18.6). Какую скорость будет иметь шарик в нижней точке траектории?

+q m l 2l	Рис. 18.6	Решение. Прежде всего, заметим, что начальное расстояние между шариками а легко вычислить по теореме Пифагора: 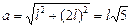. Теперь применим закон сохранения энергии: Едо = Епосле.
υ = ?

Так как

Е_до = mg×2l + ;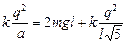

Е_после = 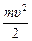+ mgl + ,

получим

Е_до = Е_после Þ 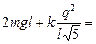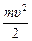+ mgl + ,

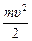= mgl + 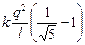Þ

.

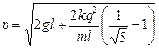Ответ: .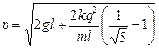

СТОП! Решите самостоятельно: С7, С10, D3.