Встречное движение зарядов

Задача 19.3. Два электрона, первоначально удаленные друг от друга на бесконечно большое расстояние, начинают двигаться со скоростью υ₀ = 1000 м/с навстречу друг другу вдоль прямой, соединяющей из центры. Определить минимальное расстояние, на которое сблизятся электроны.

υ0 = 1000 м/с т = 9,1×10–31 кг q = 1,6×10–19 Кл	Решение. Воспользуемся законом сохранения энергии: Wдо = Wпосле Þ 2 = ,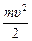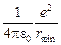
rmin­ = ?

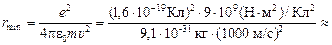
» 2,5×10^–4 м = 0,25 мм.

Ответ: 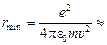0,25 мм.

Задача 19.4. Два электрона находятся друг от друга на бесконечно большом расстоянии, причем один электрон вначале покоится, а другой имеет скорость υ, направленную к центру первого (рис. 19.3). Масса электрона т, заряд е. Определить наименьшее расстояние, на которое они сблизятся.

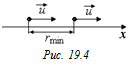
υ е т	Рис. 19.3 Решение. В момент наибольшего сближения электроны должны иметь одинаковые скорости, т.е. их относительная скорость должна равняться нулю (иначе либо они еще сближаются, либо уже разбегаются) (рис. 19.4).
rmin­ = ?

Применим закон сохранения энергии

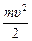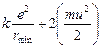= (1)

и закон сохранения импульса:

тυ = ти + ти Þ .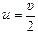

Подставим значение и в формулу (1) и получим

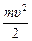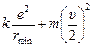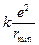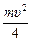= Þ = Þ .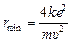

Ответ: .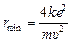

Эту задачу можно решить и другим способом. Вспомним, что такое центр масс (или центр инерции). Пусть имеется N точечных масс т₁, т₂, …, т_i,…, т_N, положение каждой из которых определяется радиусом-вектором 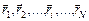. Тогда точка, положение которой задается радиусом-вектором,

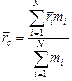(19.1)

называется центром масс (центром инерции) данной системы.

Если все частицы движутся с произвольными скоростями 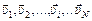, то скорость центра масс равна

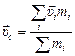. (19.2)

Этот результат легко получается простым дифференцированием:

,

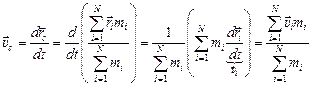что и требовалось доказать. (Попробуйте доказать это утверждение без помощи высшей математики. Для этого рассмотрите два момента времени t и t + Dt, затем с помощью формулы (19.1) найдите 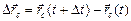, а потом вычислите .)

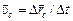Чем полезен центр масс?

1. Если система изолирована от внешних воздействий, то 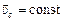. В самом деле, 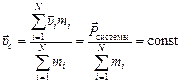(так как в замкнутой системе 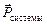= const согласно закону сохранения импульса).

2. Если перейти в систему отсчета (с.о.), связанную с центром масс, то суммарный импульс системы тел в ней будет равен нулю: 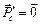. В самом деле, пусть 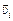– скорость i-й частицы в лабораторной с.о., а 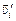– скорость этой же частицы в с.о. центра масс, тогда

,

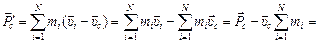
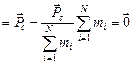что и требовалось доказать.

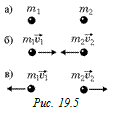Вывод: в с.о. центра масс две взаимодействующие частицы могут либо покоится, либо двигаться в противоположных направлениях, причем 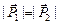, т.е. возможны только три варианта, показанные на рис. 19.5.

Вернемся к нашей задаче. Перейдем в с.о. центра масс и найдем проекцию скорости центра масс на ось х:

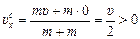
и проекции скоростей электронов на ось х:

; .

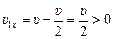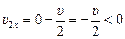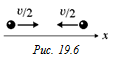То есть электроны движутся навстречу друг другу с равными скоростями (рис. 19.6). А такую задачу решить не сложно. Ясно, что скорости частиц в момент наибольшего сближения будут равны нулю. Воспользуемся законом сохранения энергии:

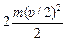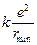= или = ,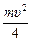

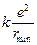откуда получаем ответ:

.

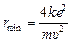СТОП! Решите самостоятельно: В7, В8, С10.

Задача 19.5. С большого расстояния навстречу друг другу со скоростью соответственно υ₁ и υ₂ движутся два электрона. Определить минимальное расстояние, на которое они сблизятся (рис. 19.7).

е т υ1 υ2	Рис. 19.7 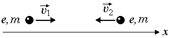Решение. Проекции скорости электронов на ось х равны: υ1х = υ1, υ2х = –υ2. Перейдем в с.о. центра масс. Проекция скорости центра масс равна
rmin­ = ?

.

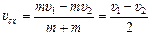Проекции скоростей электронов в с.о. центра масс равны

,

.

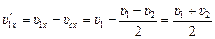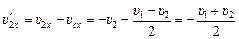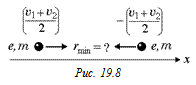Далее задача сводится к условию (рис. 19.8), по которому мы решали предыдущую задачу.

Применим закон сохранения энергии:

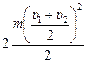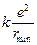= или = ,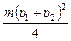

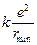откуда получаем ответ: .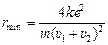

СТОП! Решите самостоятельно: С7, С8.