Задачи очень трудные. D1. В углах квадрата со стороной а по диагонали поместили два протона и два позитрона

D1. В углах квадрата со стороной а по диагонали поместили два протона и два позитрона. Оцените отношение скоростей протонов и позитронов на бесконечности. Масса протона в 1840 раз больше массы позитрона, а заряды одинаковы.

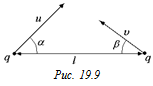D2. Две одинаковые частицы с зарядом q и скоростями и и υ, лежащими в одной плоскости, составляющими соответственно углы a и b с линией, их соединяющей, находятся на расстоянии l друг от друга (рис. 19.9). Определите массу частиц, если известно, что минимальное расстояние, на которое они сближаются, равно r.

D3. Два заряда поместили на расстоянии l друг от друга и отпустили. Через время t₀ расстояние между зарядами удвоилось. Эти же заряды поместили на расстоянии 3l и отпустили. Через какое время расстояние между зарядами удвоится?

D4. Два электрона находятся на расстоянии r друг от друга, причем скорость одного из них равна нулю, а скорость другого направлена под острым углом к линии, соединяющей электроны. Каким будет угол между скоростями электронов, когда они вновь окажутся на расстоянии r друг от друга?

D5. Две одинаковые капли ртути радиуса R летят навстречу друг другу, имея на большом расстоянии скорость υ. Происходит столкновение, в результате которого капли сливаются в одну. Определите количество выделившейся при столкновении теплоты, если: а) капли имеют разноименные заряды Q и –Q; б) одна капля имеет заряд q, другая Q. Плотность ртути r, поверхностное натяжение s.

D6. Частица массы т, имеющая заряд q, приближается с большого расстояния к равномерно заряженному незакрепленному шару, двигаясь по направлению к центру шара. Радиус шара R, заряд Q, масса М. Вначале шар покоится. Какую наименьшую скорость должна иметь частица на большом расстоянии от шара, чтобы пройти через его центр?

D7. В тонкостенной непроводящей равномерно заряженной сфере массы т₁ и радиуса r имеются два небольших диаметрально противоположных отверстия. Заряд сферы равен q₁. В начальный момент сфера покоится. По прямой, соединяющей отверстия, из бесконечности движется со скоростью υ частица массы т с зарядом q₂, одноименным с q₁. Найти время, в течение которого заряд q₂ будет находиться внутри сферы.

D8. Направленный поток электронов вылетает из узкой длинной щели со скоростью υ = 1,0×10³ м/с. Концентрация электронов в потоке п = =1,0×10¹⁰ м^–3. На каком расстоянии от щели ширина потока увеличится в два раза? Масса электрона т = 9,1×10^–31 кг, заряд q = 1,6×10^–19 Кл.

D9. Электрон влетает в осесимметричное электрическое поле, созданное неподвижными зарядами, и движется первоначально параллельно оси поля на расстоянии r от нее (рис. 19.10). Скорость электрона υ. Если скорость электрона и расстояние от него до оси меняются при движении в поле незначительно, то импульс, приобретенный электроном, можно оценить по формуле р_^ = eq/(2pe₀υr), где q – суммарный электрический заряд внутри цилиндрической области радиуса r. Выведите, используя теорему Гаусса, эту формулу.

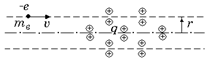
Рис. 19.10

Определите поперечный импульс, приобретенный зарядом q₁, который пролетел мимо заряда q₂. Минимальное расстояние между зарядами r, скорость заряда q₁ вначале была равна υ и менялась незначительно.

Оцените минимальное расстояние от ядра атома азота, на котором пролетал ускоренный разностью потенциалов 100 кВ электрон, если он откло­нился ядром на угол 1,0×10^–3 рад.