Логарифмический критерий устойчивости

Построение АФХ в комплексной плоскости требует трудоёмких вычислений, особенно в тех случаях, когда знаменатель передаточной функции является многочленом высокой степени. Поэтому в ряде случаев пользуются логарифмическими частотными характеристиками.

Метод основывается на возможности суждения об устойчивости замкнутой системы по взаимному расположению ЛАЧХ и ЛФЧХ системы в разомкнутом состоянии. Согласно критерию Найквиста, в случае, если система устойчива, точка 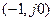лежит слева от амплитудно-фазовой характеристики первого рода.

Система будет находится на границе устойчивости, если аргумент АФХ равен 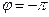, а модуль

.

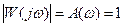При этом

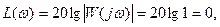
т.е. ЛАЧХ 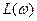пересекает ось абсцисс. Точка пересечения характеризуется частотой среза 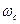(рис. 6.15, а).

Если система устойчива, то при 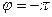величина

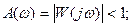
а

,

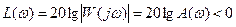т.е. ордината логарифмической амплитудной частотной характеристики будет иметь отрицательный знак (рис.6.15. б).

Для неустойчивой системы угол 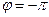соответствует

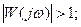
и

.

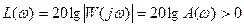В этом случае ордината ЛАЧХ будет иметь положительное значение. Либо при 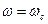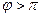(рис. 6.15, в).

Применение логарифмического критерия устойчивости даёт возможность определить влияние того или иного параметра системы на её устойчивость и переходный процесс, а также сравнительно просто определить характеристику корректирующего устройства.

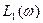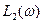Например, на рис. 6.16. показано влияние коэффициента усиления на устойчивость ЛАЧХ. и будут различны при различных коэффициентах усиления разомкнутой системы 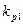и 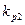, а ЛФЧХ будут совпадать. Характеристики построены для случая 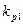> 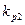. Построение частотной характеристики позволяют определить запас устойчивости по фазе

.

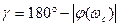и запас по устойчивости амплитуде, как число децибел, на которое нужно увеличить усиление системы, чтобы система достигла границы устойчивости.

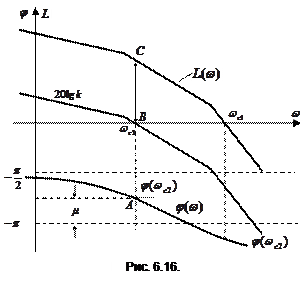
При заданном коэффициенте усиления 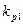логарифмические характеристики будут иметь вид кривых L(ω) и φ(ω). При частоте среза ω_с1 фаза составляет 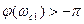, т.е. система неустойчива.

Необходимо найти такое значение коэффициента 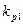, при котором обеспечивается запас по фазе, равный 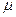. Для этого на графике откладывается значение 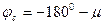, получим точку А, через которую проводим вертикаль до пересечения с частотой 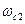на оси абсцисс. Через эту точку проводится L₂(ω) параллельно L₁(ω) . Находится новое значение коэффициента усиления 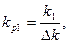где изменение коэффициента усиления 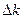определится из соотношения

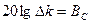дб.

Для систем, имеющих АФХ второго рода, т.е. «клювообразные» и более сложные по своей форме, практически удобнее пользоваться формулировкой логарифмического критерия устойчивости, вытекающей из правила о числе переходов. Для примера рассмотрим частотные характеристики 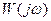и логарифмические частотные характеристик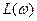и и 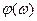для условно устойчивой системы.

На основании этих характеристик и правил о числе переходов ЛФЧХ 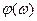через линию 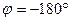логарифмический критерий устойчивости можно сформулировать следующим образом:

Система, устойчивая в разомкнутом состоянии, будет устойчивой и в замкнутом состоянии, если разность между числами положительных и отрицательных переходов ЛФЧХ 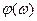через прямую 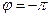равна нулю в диапазоне частот, в котором ЛФЧХ 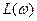положительна (рис.6.17).

На основании этого критерия система, имеющая характеристику 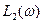- устойчива, а система, имеющая характеристику 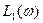(при меньшем коэффициенте усиления 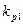) и система, имеющая характеристику 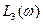(при большем 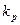) будут неустойчивыми.

С помощью критериев устойчивости можно определить, устойчива ли система при заданных её параметрах (постоянных времени, коэффициентах усиления). Однако, на практике, например при проектировании САР, часто ставится задача: при заданных параметрах за исключением одного - двух параметров, изменяющихся в широких пределах, требуется определить, при каких значениях этих параметров система устойчива. Некоторые параметры системы могут изменяться в процессе эксплуатации. В этих случаях требуется определить, будет ли устойчивой система при изменении этих параметров.

Поставленные задачи могут быть решены, если установить область возможных изменений тех или иных параметров. Для этого строятся области устойчивости.