Структурная схема САР обычно состоит из звеньев, которые выбираются в соответствии с требуемыми статическими и динамическими характеристиками этой системы.

Однако, как указывалось ранее, в состав САР могут входить и другие звенья, например, консервативное звено с положительным и отрицательным статизмом, а также звенья первого и второго порядков с отрицательным статизмом, формирующие звенья и др., имеющие соответственно следующие передаточные функции:

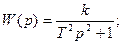
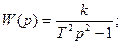
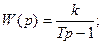
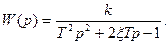
Звенья с отрицательным статизмом относятся к группе неустойчивых. Если разомкнутая система неустойчива или находится на границе устойчивости, то её характеристическое уравнение имеет корни, находящиеся в правой полуплоскости, или на мнимой оси. Это значит, что знаменатель оператора разомкнутой системы может содержать множитель типа (Tp-1).

Если в схеме САР содержатся интегрирующие звенья, то знаменатель оператора разомкнутой системы содержит и множители p, т.е. имеет корни, находящиеся на мнимой оси. Поэтому и в данном случае можно считать, что разомкнутая система находится на границе устойчивости или, как иногда говорят, нейтральна.

Структурно устойчивойназывается такая система, которая может быть сделана устойчивой путём выбора соответствующих параметров без изменения её структуры.

Структурно неустойчивая система будет неустойчивой при любых значениях параметров, и её можно сделать устойчивой, только изменяя структурную схему.

Можно показать, что система, содержащая последовательно соединенные инерционные, колебательные и интегрирующие звенья, будет после замыкания структурно неустойчивой в том случае:

1) если она содержит более одного интегрирующего звена или неустойчивого инерционного звена;

2) если число содержащихся в ней неустойчивых колебательных, или консервативных звеньев таковы, что степень характеристического уравнения не превосходит 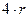, т.е. если имеет место условие ;

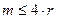3) если система содержит одно интегрирующее и одно неустойчивое инерционное звено.

Рассмотрим примеры структурных схем структурно неустойчивых (рис.6.18, а и б) и структурно устойчивой (рис.6.18, в). В схеме (рис.6.18, а) неустойчивым является консервативное звено, которое даёт незатухающие колебания и которое дает сдвиг по фазе между входным и выходным сигналами, равный –180⁰ . Поэтому система будет неустойчивой.

В схеме (рис.6.18, б) имеется два интегрирующих звена, каждое из которых дает сдвиг по фазе, равный –90⁰ , поэтому эта система также является неустойчивой.

Для схемы (рис.6.18, в), имеющей в своем составе инерционное и колебательное звенья, можно подобрать соответствующие параметры, при которых будет выполняться условие Гурвица. Т.е. система будет устойчивой.

Контрольные вопросы для самопроверки

1. Сформулируйте и объясните понятие «устойчивости САР».

2. Сформулируйте теоремы Ляпунова об устойчивости линеаризованной системы и объясните их значения для теории автоматического регулирования.

3. Зависит ли устойчивость системы от начальных значений переменных и от внешних воздействий?

4. Что такое критерий устойчивости, и чем вызвана необходимость в критериях?

5. В каких случаях целесообразно применять алгебраические критерии устойчивости?

6. Сформулируйте частотный критерий устойчивости Найквиста.

7. Почему нельзя неограниченно уменьшать статическую погрешность одноконтурной САР?

8. Что такое критический коэффициент усиления, и от чего он зависит?

9. Как формулируется критерий устойчивости по логарифмическим частотным характеристикам, устойчивой и неустойчивой в разомкнутом состоянии? Следствием какого критерия устойчивости является этот критерий?

10. Объясните понятие запаса устойчивости САР по фазе и амплитуде.

11. На что влияет запас устойчивости по фазе и амплитуде?

12. Какая связь существует между расположением корней характеристического уравнения на комплексной плоскости и устойчивостью САР?

13. Как определить и предусмотреть необходимый запас устойчивости по АФХ W(jω) и по логарифмическим частотным характеристикам L(ω) и φ(ω)?

14. Какими свойствами обладают структурно устойчивые и структурно неустойчивые системы?

ГЛАВА 7. КАЧЕСТВО СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ. КОРРЕКЦИЯ САР