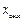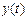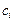Понятия и условия устойчивости

При проектировании системы управления ключевой проблемой является обеспечение её устойчивости, т.к. устойчивость является важнейшей характеристикой любой САР. С практической точки зрения неустойчивая система не имеет никакого смысла, т.к. только устойчивая система работоспособна.

Любая система управления испытывает внешние воздействия. Эти воздействия имеют различный характер и природу (задающие, возмущающие…). Всякие воздействия стремятся вывести систему из исходного состояния равновесия. Устойчивая система при этом переходит в новое устойчивое состояние равновесия.

Следовательно, под устойчивостью можно понимать свойство системы возвращаться в исходный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия.

Замкнутая САР из-за наличия обратных связей склонна к неустойчивой работе. В процессе регулирования часть энергии с выхода передаётся на вход группы звеньев системы, среди которых могут быть и колебательные звенья. При работе системы в этом случае могут возникнуть колебания регулируемой величины и её отклонение от заданного значения. Наличие главной обратной связи будет способствовать поддержанию колебательного процесса и при больших коэффициентах усиления. Если параметры системы не обеспечивают необходимого затухания (рассеивания) энергии колебаний, то это может привести к неустойчивой работе, характеризуемой возрастанием амплитуды колебаний.

В устойчивых системах энергия колебаний с течением времени уменьшается, стремясь рассеяться в виде тепловой энергии, а колебания регулируемой величины, возникшие в результате возмущения, затухают. Следовательно, в результате возмущающих воздействий и следующих за ними регулирующих воздействий регулятора, в системе возникают переходные процессы.

При этом могут иметь место три вида переходных процессов.

1. Сходящийся переходный процесс, когда регулируемая величина, отклонившись под действием возмущающих воздействий от заданного значения, с течением времени под воздействием регулятора возвращается к заданному значению. Система, имеющая такой переходный процесс, будет называться устойчивой.

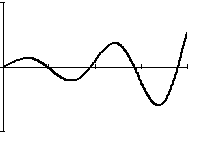
2. Расходящийся переходный процесс (рис. 6.1., б), когда регулируемая величина, отклонившись под действием возмущающих воздействий от заданного значения, с течением времени беспредельно удаляется от заданного значения. Этот процесс может быть апериодическим (кривая 1), или колебательным (кривая 2). Система, имеющая такой переходный процесс, будет неустойчивой.

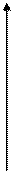
3.

В реальных условиях не может произойти беспредельное отклонение какого-либо физического параметра от заданного значения, также как и невозможны колебания с беспредельно возрастающей амплитуды из-за насыщения элементов, ограниченной мощности элементов и др.

4.Колебательный установившейся переходный процесс, когда регулируемая величина, отклонившись в результате возмущающих воздействий, от заданного значения с течением времени к установившемуся значению не возвращается, а совершает незатухающие колебания с амплитудой, зависящей от начальных условий. Линейная САР в этом случае находится на границе устойчивости.

Рассмотрение понятия устойчивости определяет устойчивость установившегося режима системы. Но система может работать в условиях непрерывно изменяющихся воздействий, когда установившийся режим вообще отсутствует.

В этом случае можно дать следующее определение устойчивости:

система устойчива, если её выходная величина остаётся ограниченной в условиях действия на систему ограниченных по величине возмущений

или иначе

устойчивая система – это динамическая система, обладающая ограниченной реакцией на ограниченный входной сигнал.

Нетрудно показать, что если переходный процесс в системе является затухающим, то система будет удовлетворять и последнему определению.

Чтобы определить устойчиво ли равновесие какой-либо статической системы, изучают её поведение при малых отклонениях от положения равновесия. Устойчивость системы при бесконечно малых отклонениях называется устойчивостью в малом. Часто системы, устойчивые в малом, оказываются устойчивыми и при конечных достаточно больших отклонениях, т.е. система оказывается устойчивой в большом.

При исследовании САР рассматривают устойчивость в малом, т.е. поведение системы при малых отклонениях регулируемой величины от установившегося значения. В линейных системах устойчивость в малом обеспечивает устойчивость и в большом.

Понятие «устойчивость» в математической трактовке впервые ввёл в науку русский учёный А.М. Ляпунов (1892 г.). Он дал стройную и законченную постановку задачи об устойчивости движения и методы её решения.

А.М. Ляпуновым были сформулированы следующие теоремы:

Теорема первая. Если вещественные части всех корней характеристического уравнения первого приближения отрицательны, то система будет устойчива независимо от членов разложения выше первого порядка малости.

Теорема вторая. Если среди корней характеристического уравнения первого приближения найдётся, по меньшей мере один с положительной вещественной частью, то система будет неустойчивой независимо от членов разложения выше первого порядка малости.

Пусть, например, свободное движение линейной САР, выведенной малым отклонением из состояния равновесия, описывается дифференциальным уравнением замкнутой системы

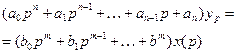(6.1)

Т.е. в общем случае передаточная функция линейной САР

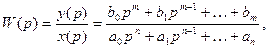(6.2)

где .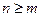

Первая часть дифференциального уравнения определяется внешними воздействиями. Об устойчивости системы можно судить по переходному процессу при приложении внешних воздействий

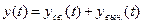(6.3)

Для устойчивых систем правая часть определяет значение регулируемой координаты 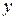в статическом режиме.

Свободная составляющая:

,

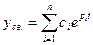где: 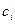– постоянная интегрирования;

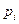– корни характеристического уравнения.

Вынужденная составляющая (при p=0):

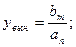
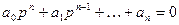. (6.4)

Характеристическое уравнение или характеристический полином – это знаменатель передаточной функции по задающему, возмущающему воздействию или по ошибке регулирования.

Вынужденная составляющая представляет собой частное решение уравнения, является полезной составляющей регулируемой величины. Она характеризует установившийся режим системы. Переходная или свободная составляющая является решением однородного дифференциального уравнения и имеет место в переходном режиме. Эта составляющая по существу представляет ошибку системы в переходном режиме (отклонение системы от равновесного состояния) и поэтому является нежелательной составляющей регулируемой величины. Переходная составляющая (решение однородного уравнения) в случае некратных корней может быть представлена в виде следующей суммы:

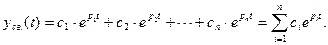(6.5)

Очевидно, что система будет устойчивой, если переходная составляющая 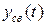в ней с течением времени затухает, т.е. решение уравнения (6.5) должно удовлетворять требованию:

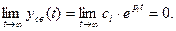(6.6)

Если же 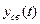при 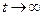не стремится к нулю, а возрастает или представляет незатухающие колебания, то система неустойчива.

Из формулы (6.6) видно, что затухание 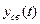, т.е. устойчивость системы, зависит от значения корней 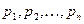характеристического уравнения замкнутой системы (6.4).

Возможны следующие случаи:

Корни вещественные

Если все корни отрицательные, то с течением времени все члены уравнения (6.6), содержащие множитель 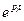стремится к нулю, т.к. 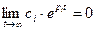, а отклонение регулируемой величины 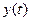стремится к постоянному значению 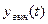или к нулю. Система в этом случае устойчива.

Если хотя бы один из корней, например, p₁ положителен, то соответствующий член 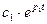с течением времени неограниченно возрастает, и отклонение регулируемой величины 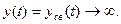Система в этом случае будет неустойчивой.

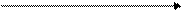
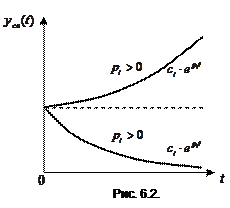Если все вещественные кони отрицательны, то каждая составляющая или множитель 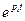стремятся к нулю при 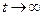, т.е.

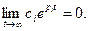
Если же вещественные части корней положительны 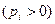, то

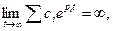
и система неустойчивая.

2.Корни комплексные сопряжённые с отрицательной вещественной частью

;

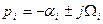В этом случае

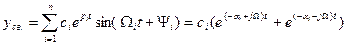(6.7)

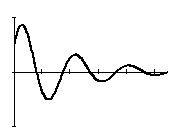
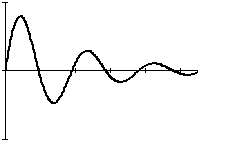
Если корни сопряженные комплексные, то в этом случае при отрицательных вещественных частей отклонение регулируемой величины приходит к установившемуся значению (к нулю) с затухающими гармоническими колебаниями.

Действительно, если вещественные части 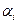всех комплексных корней отрицательны, то каждое слагаемое суммы (6.8) представляет собой затухающее колебание и поэтому

,

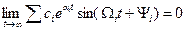т.е. система устойчивая.

3.Корни комплексные сопряжённые при положительной вещественной части.

.

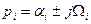Если хотя бы одна пара комплексных корней имеет положительную вещественную часть ( 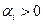), то в этом случае

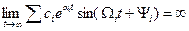(6.8)

отклонение регулируемой величины совершает колебания с неограниченно возрастающей амплитудой. Система неустойчива.

4.Корни имеют нулевую вещественную часть ( 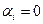), т. е.

.

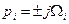В этом случае отклонение регулируемой величины совершает незатухающие колебания (автоколебания), т.е. система находится на границе устойчивости

Таким образом, условием устойчивости системы автоматического управления является отрицательность вещественных частей всех корней характеристического уравнения (т. е. расположение всех корней характеристического уравнения в левой полуплоскости комплексной плоскости корней.)

Корни характеристического уравнения замкнутой системы зависят только от параметров системы (коэффициентов уравнения 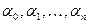), т. е. от постоянных времени и коэффициентов усиления звеньев.

Корни характеристического уравнения можно представить в виде векторов, расположенных в комплексной плоскости. Очевидно, что система будет устойчивой, если все корни располагаются слева от мнимой оси.

В случае если один вещественный корень или пара комплексно сопряженных корней располагается на мнимой оси, система оказывается на границе устойчивости. Системы, у которых имеется одна пара мнимых корней, могут совершать незатухающие колебания (автоколебания). Если система имеет один нулевой корень при всех остальных корнях, расположенных левее мнимой оси, называют нейтрально устойчивыми.

Для того чтобы все корни оказались в левой полуплоскости, можно воздействовать на коэффициенты характеристического уравнения, которые связаны с корнями непрерывными зависимостями.

Задача определения устойчивости может быть решена различными методами. Можно определять корни характеристического уравнения и по ним устанавливать знаки вещественных частей. Но такой метод может быть использован, когда порядок характеристического уравнения ниже третьего. Уравнения более высоких степеней вообще не имеют аналитического решения и могут быть решены лишь приближенно.

Но для определения устойчивости совершенно не обязательно знать значение корней. Достаточно убедиться только в отрицательности вещественных частей корней. Для этого можно воспользоваться методами, основанными на использовании критериев устойчивости.

Критерием устойчивости называется косвенный метод определения знаков вещественной части корней характеристического уравнения, не требующий решения этого уравнения.

Все известные критерии делятся на 2 группы:

1) алгебраические,

2) частотные.

К алгебраическим относятся критерии: Вышнеградского, Рауса, Гурвица. К частотным относятся критерии Михайлова, Найквиста, логарифмический критерий устойчивости. Особое место занимает выделение областей устойчивости. Применение того или иного критерия зависит от конкретных условий.

6.2. Алгебраический критерий устойчивости Рауса – Гурвица

Алгебраические критерии устойчивости позволяют установить, устойчива система или нет, по результатам алгебраических действий над коэффициентами характеристического уравнения. Впервые вопрос устойчивости динамических систем был исследован Максвеллом и Вышнеградским. В конце XIX века А. Гурвиц и Э.Дж. Раус независимо друг от друга опубликовали работы, посвященные методу анализа устойчивости линейных систем. Критерий Рауса – Гурвица позволяет ответить на вопрос об устойчивости путём анализа характеристического уравнения системы, записанного в виде (6.4).

Для ответа на поставленный вопрос необходимо установить, находится ли хотя бы один из корней этого уравнения в правой половине комплексной плоскости.

Анализ характеристического уравнения показывает, что если все корни расположены в левой полуплоскости, то все коэффициенты характеристического полинома должны иметь один и тот же знак. Необходимо также, чтобы все коэффициенты были отличны от нуля (если система устойчива). Однако, эти условия являются лишь необходимыми, но не достаточными. Это означает, что если данные условия не выполняются, то сразу можно сказать, что система неустойчива; но если даже эти условия выполняются, то для ответа на вопрос об устойчивости системы необходимы дальнейшие исследования.

Критерий Рауса – Гурвица даёт необходимое и достаточное условие устойчивости линейных систем. Первоначально он был предложен в форме определителей, в соответствии с которыми для получения отрицательных вещественной части всех корней характеристического уравнения r-й степени, необходимо и достаточно, чтобы при 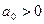все n-определителей Гурвица были положительными, а затем в более удобной табличной форме.

В настоящее время применение алгебраических критериев не актуально. Ознакомиться подробнее с этими критериями можно в любом учебнике по ТАУ.