Применение астатической системы управления

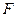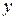Статическое отклонение будет равно нулю, если в рассматриваемую статическую САР ввести интегрирующее звено так, чтобы оно находилось вне участка системы от места приложения до , т. е. чтобы его передаточная функция 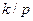не входила в 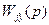. В этом случае в соответствии с (5.7) 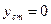, т. к. при конечном значении 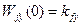будем иметь 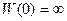из-за наличия в знаменателе p в связи с появлением передаточной функции 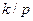интегрирующего звена. Если же интегрирующее звено находится между точкам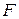и и 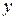, т. е. в составе передаточной функции 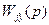, статическое отклонение не устраняется.

Действительно,

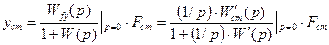
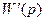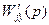Здесь и – передаточные функци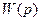и и 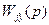после выделения из них множителя p в знаменателе.

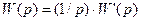и ,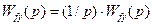

причём 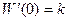и .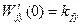

Отсюда

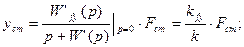(5.8)

т. е. в данном случае существует статизм системы

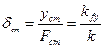. (5.9)

Таким образом, условием устранения статического отклонения 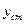является наличие интегрирующего звена в системе вне участка, описываемого передаточной функцией 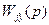. САР, приведённая к одноконтурному виду и имеющая в своём составе интегрирующее звено, будет называться астатической. Если интегрирующее звено находится в управляющем устройстве, все возмущения, приложенные к объекту управления, не будут создавать статического отклонения его выходной величины 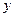. Если же интегрирующее звено находится в объекте управления, все возмущения, приложенные ко входу объекта, будут вызывать статическое отклонение 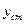, определяемое выражением (5.9). В то же время статическая ошибка 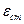, вызванная задающим воздействием, будет устраняться и за счёт астатизма объекта.

Действительно

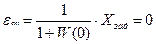. (5.10)

Можно также показать, что если 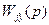содержит интегрирующее звено, статическое отклонение также будет устранено при введении интегрирующего звена вне этой передаточной функции.

Для устранения статического отклонения 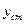от возможно большего числа возмущений, действующих на систему, желательно вводить интегрирующее звено в управляющее устройство и помещать его возможно ближе ко входу последнего, т. е. дальше от .

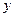Аналогичный вывод можно сделать и для САР, когда статическая ошибка 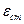вызвана задающим воздействием 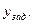В этом случае 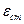устраняется и за счет астатизма объекта.

Действительно

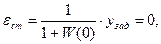
поскольку передаточная функция интегрирующего звена не входит в числитель этого выражения.

В связи с усложнением астатической системы переход к ней целесообразен только в случае, когда для получения заданной статической точности требуется достаточно большой коэффициент передачи статической системы, что также затруднительно.

5.3.2. Устранение статического отклонения введением компенсирующего воздействия

Рассматриваемый путь устранения статического отклонения заключается в обращении в нуль числителя выражения (5.7) при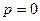

,

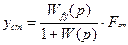т. е. в получении .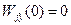

Такой результат может быть получен, если использовать управление по возмущению. Суть способа заключается в том, что сигнал, пропорциональный измеренному внешнему возмущению, подаётся на управляющее устройство, которое осуществляет такое воздействие на объект управления, чтобы компенсировать естественное влияние данного возмущения на выходную регулируемую величину объекта.

Схема системы компенсации возмущений показана на рис. 5.2.

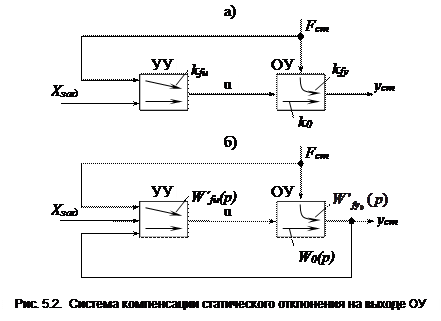
В соответствии со схемой разомкнутой САР (рис.5.2,а) условия компенсации возмущений 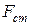на статическое отклонение 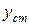будет иметь следующий вид

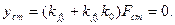(5.11)

Из этого выражения может быть найден коэффициент передачи управляющего устройства по возмущению

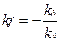. (5.12)

Следовательно, этот коэффициент зависит от параметров объекта управления. Последнее выражение (5.12) определяет коэффициент передачи управляющего устройства УУ в зависимости от параметров объекта управления ОУ, при котором 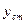не зависит от .

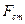На рис. 5.2.б изображена комбинированная САУ. В ней замкнутая САУ, рассмотренная ранее, дополнена разомкнутой системой компенсации возмущения 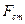на 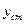. В этой системе

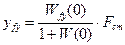, (5.13)

где

.

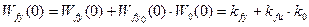При выполнении условия (5.12) 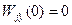, поэтому с точки зрения статики замкнутая система освобождена от влияния возмущения .

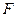Компенсация может быть также применена к возмущениям, действующим не только на объект управления, но и на любое звено управляющего устройства. Компенсация возмущений не делает систему астатической, т. к. другие, не скомпенсированные возмущения по-прежнему создают статическое отклонение 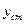. Однако, такая компенсация позволяет резко снизить суммарное статическое отклонение 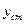, вызванное всеми возмущениями, которое определится формулой

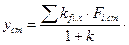(5.14)

В этом случае из числителя этого выражения исключается одно из слагаемых. Величина статического отклонения при этом может быть снижена на порядок, если компенсация осуществляется по наиболее сильно влияющему на 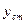возмущению.