Изгибные колебания трубопровода с движущейся жидкостью.
Выведем дифференциальное уравнение малых изгибных колебаний призматической балки (трубы) конечной длины 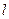 , изгибной жесткостью
, изгибной жесткостью 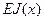 с внутренним стационарным потоком идеальной несжимаемой жидкости, движущейся с постоянной скоростью
с внутренним стационарным потоком идеальной несжимаемой жидкости, движущейся с постоянной скоростью 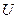 относительно стенок трубы. При исследовании изгибных колебаний трубы с протекающей внутри жидкостью воспользуемся моделью в виде непризматической балки и гипотезой плоских сечений. В этом случае для анализа колебаний справедлива формула из параграфа 5.8
относительно стенок трубы. При исследовании изгибных колебаний трубы с протекающей внутри жидкостью воспользуемся моделью в виде непризматической балки и гипотезой плоских сечений. В этом случае для анализа колебаний справедлива формула из параграфа 5.8
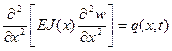 , (5.61)
, (5.61)
где 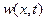 - уравнение упругой оси балки относительно ее недеформированного состояния при действии поперечной заданной нагрузки
- уравнение упругой оси балки относительно ее недеформированного состояния при действии поперечной заданной нагрузки 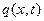 .
.
Пусть вдоль оси трубы будут неизменны ее изгибная жесткость 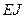 , масса единицы длины трубы
, масса единицы длины трубы 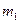 и масса объема жидкости
и масса объема жидкости 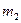 , заполняющего единицу длины трубы. В соответствии с принципом Даламбера возникающие при колебаниях силы инерции (рис. 5.16) можно считать для балки поперечной нагрузкой, тогда
, заполняющего единицу длины трубы. В соответствии с принципом Даламбера возникающие при колебаниях силы инерции (рис. 5.16) можно считать для балки поперечной нагрузкой, тогда
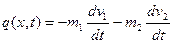 ,
,
где 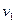 - абсолютная скорость элемента трубы, а
- абсолютная скорость элемента трубы, а 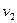 - абсолютная скорость элемента протекающей жидкости.
- абсолютная скорость элемента протекающей жидкости.

Рис.5.16
Для стационарного потока давление вдоль оси трубы не изменяется, а скорость движения жидкости 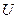 не зависит от колебаний трубы. Тогда инерционная нагрузка может быть записана в виде
не зависит от колебаний трубы. Тогда инерционная нагрузка может быть записана в виде
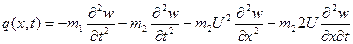 . (5.62)
. (5.62)
Здесь первое слагаемое – сила инерции элемента трубы, возникающая при его поперечных колебаниях; поскольку элемент жидкости совершает сложное движении (переносное движение со скоростью 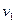 элемента трубы, относительное - со скоростью
элемента трубы, относительное - со скоростью 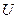 ), остальные слагаемые в (5.62) отражают его силы инерции – силу инерции переносного движения, нормальную составляющую силы инерции относительного движения и силу инерции Кориолиса, соответственно. При вычислении составляющих ускорения элемента жидкости учтено, что кривизна балки
), остальные слагаемые в (5.62) отражают его силы инерции – силу инерции переносного движения, нормальную составляющую силы инерции относительного движения и силу инерции Кориолиса, соответственно. При вычислении составляющих ускорения элемента жидкости учтено, что кривизна балки 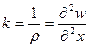 , угол поворота элемента
, угол поворота элемента 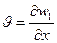 , а его угловая скорость
, а его угловая скорость 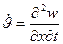 .
.
Подставив (5.62) в (5.61), получим дифференциальное уравнение поперечных колебаний оси трубопровода относительно начального прямолинейного положения:
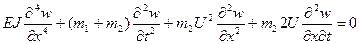 . (5.63)
. (5.63)
Решение уравнения (5.63) можно получить одним из приближенных аналитических методов (см. параграф 5.10). Воспользуемся методом Бубнова – Галеркина, представив решение уравнения в виде произведения двух функций
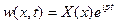 . (5.64)
. (5.64)
Решение (5.64) должно удовлетворять четырем граничным условиям, соответствующим вариантам закрепления концов трубопровода (см. параграф 5.8).
Подстановка (5.64) в (5.63) позволит для функции 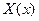 получить обыкновенное дифференциальное уравнение:
получить обыкновенное дифференциальное уравнение:
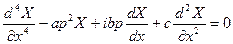 , (5.65)
, (5.65)
где 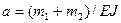 ,
, 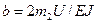 ,
, 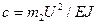 ,
, 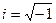 .
.
Решение уравнения (5.65) будем искать в виде 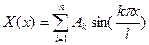 , подстановка которого в уравнения (5.64) с последующим умножением на
, подстановка которого в уравнения (5.64) с последующим умножением на 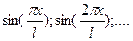 и интегрированием при граничных условиях от
и интегрированием при граничных условиях от 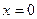 до
до 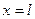 , приводит к системе линейных однородных уравнений относительно неизвестных постоянных
, приводит к системе линейных однородных уравнений относительно неизвестных постоянных 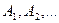 Приравняв определитель системы к нулю, получим уравнение для определения частот колебаний трубопровода
Приравняв определитель системы к нулю, получим уравнение для определения частот колебаний трубопровода 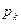 .
.
При исследовании возникающих колебаний представляет интерес ответ на вопрос о значении критической скорости 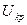 потока жидкости (скорость протекания жидкости, при которой трубопровод может потерять статическую устойчивость). Это значение можно найти из условия равенства нулю первой частоты колебаний (что, в свою очередь, имеет место при равенстве нулю слагаемого, не содержащего частоту в уравнении для определения частот).
потока жидкости (скорость протекания жидкости, при которой трубопровод может потерять статическую устойчивость). Это значение можно найти из условия равенства нулю первой частоты колебаний (что, в свою очередь, имеет место при равенстве нулю слагаемого, не содержащего частоту в уравнении для определения частот).
Пример 9 [11].По участку трубопровода с шарнирными опорами на концах (см. рис. 5.17), течет с постоянной скоростью 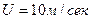 идеальная несжимаемая жидкость. Средний диаметр сечения трубопровода
идеальная несжимаемая жидкость. Средний диаметр сечения трубопровода 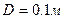 , толщина стенки трубопровода
, толщина стенки трубопровода 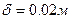 , длина участка
, длина участка 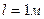 , плотность материала
, плотность материала 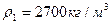 , модуль упругости
, модуль упругости 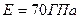 . Масса жидкости
. Масса жидкости 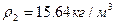 . Определить первые две частоты поперечных колебаний трубопровода с покоящейся и протекающей жидкостью без учета действия статических сил веса.
. Определить первые две частоты поперечных колебаний трубопровода с покоящейся и протекающей жидкостью без учета действия статических сил веса.

Рис.5.17
Решение:
Воспользуемся дифференциальным уравнением (5.63) , где 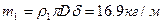 - масса единицы длины трубы, а
- масса единицы длины трубы, а 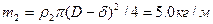 - масса единицы длины жидкости. Для получения решения воспользуемся методом Бубнова – Галеркина. Полагая что
- масса единицы длины жидкости. Для получения решения воспользуемся методом Бубнова – Галеркина. Полагая что 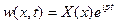 , после подстановки предполагаемого решения в (5.63) и выполнения достаточно несложных преобразований, для уравнения (5.65) получим значения коэффициентов
, после подстановки предполагаемого решения в (5.63) и выполнения достаточно несложных преобразований, для уравнения (5.65) получим значения коэффициентов 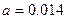 ,
, 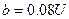 ,
, 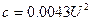 . Решение уравнения (5.65) должно удовлетворять граничным условиям:
. Решение уравнения (5.65) должно удовлетворять граничным условиям:
При 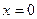 :
: 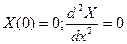 , при
, при 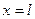 :
: 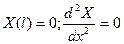 .
.
Ищем решение уравнения (5.65) в виде 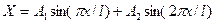 . Подставим это решение в (5.65) и последовательно умножим полученное выражение на
. Подставим это решение в (5.65) и последовательно умножим полученное выражение на 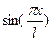 и
и 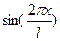 . Полученные соотношения проинтегрируем в интервале от
. Полученные соотношения проинтегрируем в интервале от 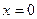 до
до 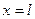 с учетом граничных условий. В результате выполненных действий приходим к алгебраической системе из двух линейных однородных уравнений относительно неизвестных
с учетом граничных условий. В результате выполненных действий приходим к алгебраической системе из двух линейных однородных уравнений относительно неизвестных 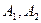 :
:
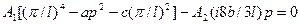 ;
;
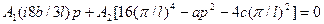 .
.
Приравнивая к нулю определитель этой системы, получим уравнение вида 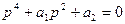 для определения двух частот поперечных колебаний трубопровода.
для определения двух частот поперечных колебаний трубопровода.
При 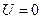
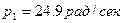 , а
, а 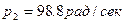 ;
;
При 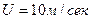
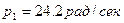 , а
, а 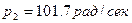 .
.
Критическая скорость протекания жидкости возникает при равенстве нулю одной из частот колебаний, что имеет место при 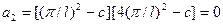 , где
, где 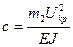 . Отсюда значение минимальной критической скорости будет
. Отсюда значение минимальной критической скорости будет 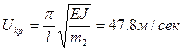 .
.
Дата добавления: 2016-02-11; просмотров: 2670;
