Энергетические методы.

В некоторых случаях нет необходимости составлять дифференциальные уравнения движения для определения частот собственных колебаний механической системы. Для определения частот можно использовать метод, основанный на энергетических соотношениях. Рассмотрим применение этого метода на примере простой механической системы (рис.5.13). Считается, что диск не проскальзывает в процессе качения.

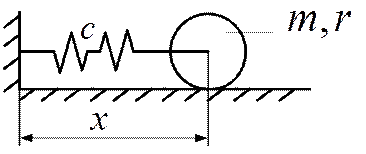
Рис.5.13.

Закон колебательного движения системы определяется выражением

.

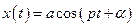При максимальном отклонении механической системы от положения равновесия потенциальная энергия достигает максимального значения

.

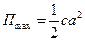При прохождении положения равновесия кинетическая энергии достигает максимума

.

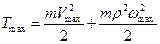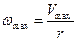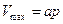Учитывая, что и , найдем

.

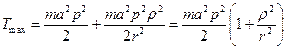Учитывая, что отсчет потенциальной энергии ведется от положения равновесия, при отсутствии диссипации энергии справедливо равенство

,

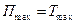откуда сразу находим

.

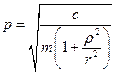Формула Рэлея.

Задавая только одну форму колебаний балки 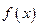с распределенной массой, мы аппроксимируем ее движение, рассматривая его как движение системы с одной степенью свободы

.

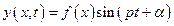При этом колебания всех поперечных сечений происходят с одной и той же фазой, все сечения балки в один и тот же момент достигают максимального отклонения 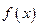от положения равновесия. Потенциальная энергия балки при таком отклонении балки будет максимальной

.

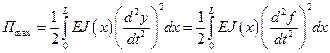Максимальная кинетическая энергия балки, совершающей колебательное движение, соответствует моменту, когда все сечения имеют максимальную скорость 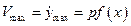, и вычисляется по формуле

.

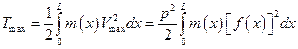Формула Релея, позволяющая вычислить собственную частоту колебаний, основана на энергетическом соотношении

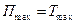
и выглядит следующим образом

.

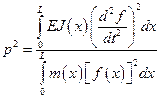Пример 7.Для балки, лежащей на упругом безынерционном основании, рис.5.14, определить первую собственную частоту колебаний методом Релея. Коэффициент жесткости основания 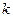, масса единицы длины 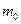, изгибная жесткость .

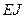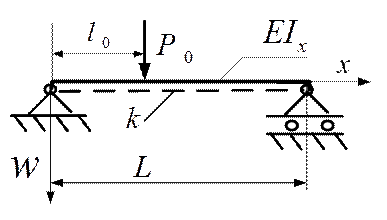Рис.5.14.

Решение:

При колебаниях балки на упругом основании на элемент балки 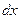действует дополнительная консервативная сила 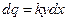, направленная против смещения 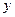. Поэтому потенциальная энергия балки будет равна ,

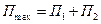где 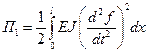- максимальная потенциальная энергия изгиба балки;

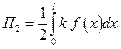- максимальная потенциальная энергия деформации упругого основания. По методу Релея:

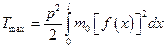- максимальная кинетическая энергия. Тогда квадрат частоты колебаний вычисляется по формуле

.

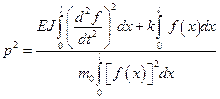Форму колебаний зададим в виде функции 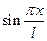, которая удовлетворяет краевым условиям задачи:

; ; ; ;

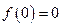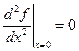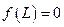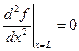После вычисления получим

.

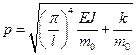Метод Ритца.

Считается, что балка движется по гармоническому закону

,

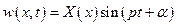где 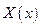- форма собственных колебаний, которую можно представить в виде разложения в ряд по базисным функциям 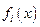, удовлетворяющим граничным условиям,

.

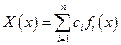Для вычисления собственной частоты применим формулу Рэлея

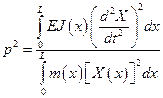. (5.54)

Идея метода Ритца состоит в следующем. Для нахождения более точного значения собственной частоты необходимо выбрать коэффициенты 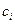таким образом, чтобы квадрат собственной частоты был минимальным, то есть должно выполняться условие

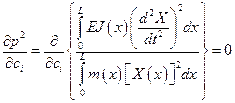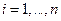; . (5.55)

Дифференцируя каждое из уравнений системы (5.55), преобразуем ее к виду

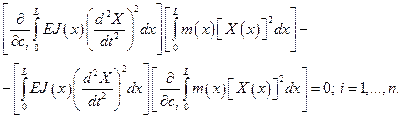
Разделив это выражение на 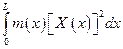и учитывая формулу (5.54), найдем

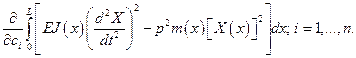
Эта система уравнений однородна относительно коэффициентов 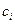. Для получения нетривиального решения приравняем определитель этой системы к нулю, полученное уравнение будет содержать только одну неизвестную величину 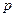- это частота собственных колебаний. Решая это уравнение можно найти значение частоты.