Изгибные колебания балок.
Используя статическую теорию изгиба балок, запишем дифференциальное уравнение изгиба упругой балки (рис.5.10), находящейся под действием поперечной погонной нагрузки 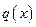
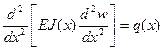 ,
,
где 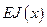 - жесткость на изгиб;
- жесткость на изгиб; 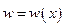 - уравнение упругой оси.
- уравнение упругой оси.
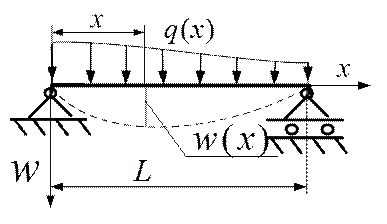
Рис.5.10.
Уравнение свободных колебаний балки можно получить, если считать, что ее прогиб 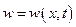 зависит от времени, интенсивность поперечной нагрузки равна силе инерции
зависит от времени, интенсивность поперечной нагрузки равна силе инерции 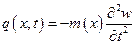 . Согласно принципу Даламбера
. Согласно принципу Даламбера
 . (5.35)
. (5.35)
Рассмотрим частный случай, когда балка является призматической: 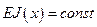 и
и 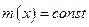 , тогда уравнение (5.35) принимает вид
, тогда уравнение (5.35) принимает вид
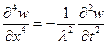 (5.36)
(5.36)
где 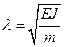 - постоянный коэффициент. Воспользуемся методом Фурье и представим решение этого уравнения в виде
- постоянный коэффициент. Воспользуемся методом Фурье и представим решение этого уравнения в виде
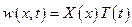 . (5.37)
. (5.37)
Подставим это решение в уравнение (5.33)
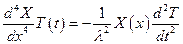
или
 .
.
Последнее уравнение в частных производных распадается на два обыкновенных дифференциальных уравнения
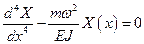 , (5.38)
, (5.38)
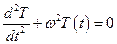 . (5.39)
. (5.39)
Для решения задачи о свободных колебаниях балки необходимо решить оба этих уравнения. Рассмотрим вначале процедуру решения уравнения (5.36), в результате найдем формы собственных колебаний балки. Используя обозначение 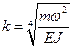 , представим решение уравнения (5.38) в форме
, представим решение уравнения (5.38) в форме
 . (5.40)
. (5.40)
Для определения постоянных используются граничные условия следующих видов:
· Свободный конец балки:  ,
, 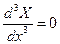 , при
, при  .
.
· Шарнирно закрепленный конец 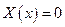 ,
,  , при
, при  .
.

· Защемленный конец балки: 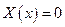 ,
, 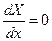 , при
, при  .
.

· Упруго опертый конец балки:  ,
, 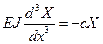 , при
, при  .
.

· Точечный груз на конце балки:  ,
,  , при
, при  .
.

При решении практических задач чаще используют решение уравнения (5.38) в другой форме
 , (5.41)
, (5.41)
где 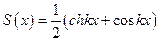 ;
;  ;
; 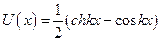 ;
; 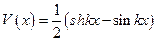 - функции Крылова. Решение (5.39) уравнения (5.38) должно удовлетворять четырем граничным условиям из перечисленных выше вариантов. Например, решение уравнения (5.38) для шарнирно опертой балки состоит в выполнении следующей процедуры. Решение (5.41) непосредственно подставляется в граничные условия
- функции Крылова. Решение (5.39) уравнения (5.38) должно удовлетворять четырем граничным условиям из перечисленных выше вариантов. Например, решение уравнения (5.38) для шарнирно опертой балки состоит в выполнении следующей процедуры. Решение (5.41) непосредственно подставляется в граничные условия
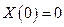 ;
; 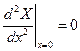 ;
; 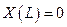 ,
, 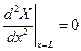 ,
,
в результате приходим к системе четырех алгебраических уравнений
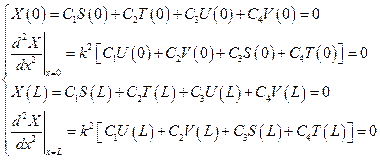
Из первых двух уравнений находим

Последние два уравнения упрощаются
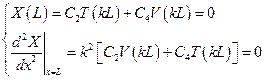 (5.42)
(5.42)
Это однородная система уравнений, которая имеет нетривиальное решение только если
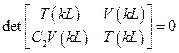
или
 . (5.43)
. (5.43)
Так как 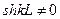 , то это уравнение упрощается
, то это уравнение упрощается
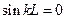 . (5.44)
. (5.44)
Его решение записывается в форме 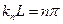 или
или 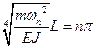 , откуда находим собственные частоты колебаний балки
, откуда находим собственные частоты колебаний балки 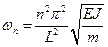 . Каждой собственной частоте
. Каждой собственной частоте 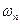 будет соответствовать одно решение системы уравнений (5.42)
будет соответствовать одно решение системы уравнений (5.42)
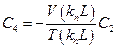 .
.
Подставляя найденные значения постоянных интегрирования  ,
, 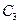 и
и 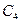 в решение (5.41), находим формы собственных колебаний шарнирно опертой балки, каждая из которых удовлетворяет граничным условиям и является решением уравнения (5.38)
в решение (5.41), находим формы собственных колебаний шарнирно опертой балки, каждая из которых удовлетворяет граничным условиям и является решением уравнения (5.38)
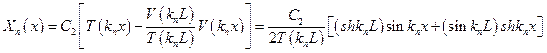 .
.
Формы собственных колебаний могут быть найдены только с точностью до постоянного множителя 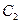 . С учетом уравнения (5.44), это выражение упрощается
. С учетом уравнения (5.44), это выражение упрощается
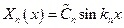 ,
,
где 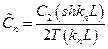 - постоянный коэффициент. Легко проверить, найденные формы колебаний удовлетворяют условию ортогональности
- постоянный коэффициент. Легко проверить, найденные формы колебаний удовлетворяют условию ортогональности
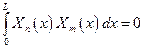 , при
, при 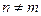 .
.
Перейдем к решению уравнения (5.39). Частное решение этого уравнения можно записать в виде
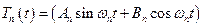 .
.
Учитывая форму записи решения (5.34) уравнения в частных производных (5.33), можно записать его частное решение в виде
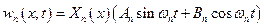 .
.
Поскольку формы собственных колебаний  образуют полную систему функций в пространстве, в котором происходит движение балки (пространство конфигураций), учитывая линейность уравнения (5.35) относительно
образуют полную систему функций в пространстве, в котором происходит движение балки (пространство конфигураций), учитывая линейность уравнения (5.35) относительно  , общее решение этого уравнения можно записать как линейную комбинацию частных решений
, общее решение этого уравнения можно записать как линейную комбинацию частных решений
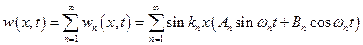 . (5.45)
. (5.45)
Постоянные коэффициенты 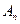 и
и 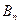 определяются из начальных условий
определяются из начальных условий
 ;
;  , (5.46)
, (5.46)
которые характеризуют начальное возмущение, являющееся причиной возникновения свободных колебаний. Непосредственная подстановка решения (5.45) в выражения (5.46) приводит к системе уравнений
 ;
; 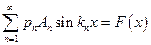 . (5.47)
. (5.47)
Если воспользоваться разложением функций 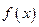 и
и 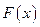 в ряд Фурье, то легко можно вычислить значения коэффициентов
в ряд Фурье, то легко можно вычислить значения коэффициентов 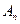 и
и 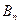 следующим путем: умножая выражения (5.47) на функцию
следующим путем: умножая выражения (5.47) на функцию  и интегрируя в пределах от
и интегрируя в пределах от 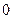 до
до 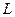 , находим
, находим
 ;
; 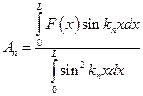 .
.
Пример 5.Определить собственные частоты малых изгибных колебаний однородной балки 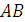 длины
длины 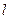 , закрепленной как показано на рисунке 5.11. Масса единицы длины
, закрепленной как показано на рисунке 5.11. Масса единицы длины 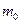 , изгибная жесткость
, изгибная жесткость  .
.
 Рис.5.11.
Рис.5.11.
Решение:
Запишем уравнение изгибных колебаний (5.36):
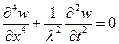 ,
,
где  - постоянный коэффициент. Запишем решение в виде
- постоянный коэффициент. Запишем решение в виде 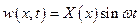 . После подстановки предполагаемого решения в дифференциальное уравнение, получим обыкновенное дифференциальное уравнение:
. После подстановки предполагаемого решения в дифференциальное уравнение, получим обыкновенное дифференциальное уравнение:
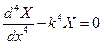 ,
,
где 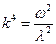 . Решение уравнения разыскиваем в виде (5.41):
. Решение уравнения разыскиваем в виде (5.41):
 ,
,
где  ;
; 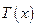 ;
;  ;
;  – функции Крылова. Подставляя решение в выражения для граничных условий
– функции Крылова. Подставляя решение в выражения для граничных условий
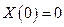 ;
; 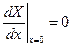 ;
; 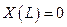 ;
; 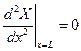 ;
;
приходим к системе однородных алгебраических уравнений относительно постоянных интегрирования  . Приравнивая определитель этой системы к нулю, приходим к частотному уравнению
. Приравнивая определитель этой системы к нулю, приходим к частотному уравнению
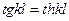 .
.
Его корни равны:
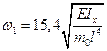 ;
; 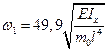 ;…;
;…; 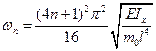 .
.
Дата добавления: 2016-02-11; просмотров: 7435;
