Решение волнового уравнения для неограниченной струны.
В математической физике эту задачу принято называть задачей Коши. Ее решение строится в виде суммы прямой и обратной бегущей волны
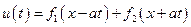 . (5.33)
. (5.33)
Непосредственной подстановкой можно убедиться, что решение (5.33) обращает волновое уравнение (5.32)в тождество при любом виде функций 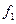 и
и 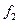 .
.
Запишем решение волнового уравнения при заданных начальных условиях:
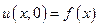 ;
; 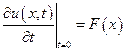 .
.
Покажем, что решение волнового уравнения
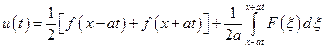
удовлетворяет заданным начальным условиям. Так как при 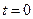 интеграл в этом выражении равен нулю, то выполняется первое начальное условие:
интеграл в этом выражении равен нулю, то выполняется первое начальное условие: 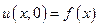 . С другой стороны
. С другой стороны
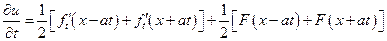 ,
,
поэтому выполняется второе начальное условие
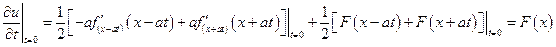 .
.
То есть задача решена.
Пример 4.Получить дифференциальное уравнение малых поперечных колебаний струны, лежащей на упругом безынерциальном основании, рис.5.9, и определить собственные частоты колебаний. Натяжение струны равно 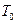 , масса единицы длины
, масса единицы длины 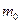 . При смещении струны из положения равновесия на нее действует восстанавливающая сила, пропорциональная смещению струны, коэффициент пропорциональности которой
. При смещении струны из положения равновесия на нее действует восстанавливающая сила, пропорциональная смещению струны, коэффициент пропорциональности которой 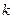 .
.

Рис.5.9.
Решение:
Воспользуемся для решения задачи уравнением (5.30). Внешняя нагрузка 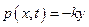 будет вызвана восстанавливающей силой со стороны упругого основания и направлена противоположно перемещению конечного элемента струны. С учетом этого, уравнение примет вид:
будет вызвана восстанавливающей силой со стороны упругого основания и направлена противоположно перемещению конечного элемента струны. С учетом этого, уравнение примет вид:
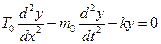
или
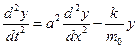 (5.34)
(5.34)
где 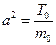 . Решение уравнение (5.34) ищем в виде
. Решение уравнение (5.34) ищем в виде 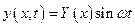 . После подстановки в (5.34) и преобразований имеем обыкновенное дифференциальное уравнение:
. После подстановки в (5.34) и преобразований имеем обыкновенное дифференциальное уравнение:
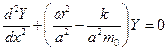
или
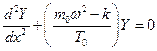 .
.
Решение этого уравнения будем искать в виде
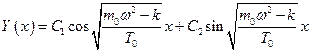
Запишем краевые условия:
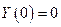 и
и 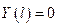 ,
,
из которых следует
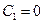 и
и 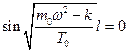
или
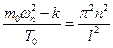 ,
, 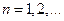 .
.
Откуда, частоты колебаний струны, лежащей на упругом основании, равны
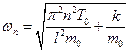 .
.
Дата добавления: 2016-02-11; просмотров: 1571;
