Метод Бубнова - Галеркина.
Рассмотрим порядок действий для нахождения собственной частоты поперечных колебаний балки.
Записывается уравнение поперечных колебаний непризматической балки
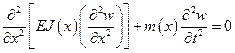 . (5.56)
. (5.56)
Его решение представляется в виде произведения двух функций  . Это позволяет свести дифференциальное уравнение в частных производных (5.56) к обыкновенному дифференциальному уравнению
. Это позволяет свести дифференциальное уравнение в частных производных (5.56) к обыкновенному дифференциальному уравнению
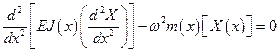 . (5.57)
. (5.57)
Решение уравнения (5.57) представляется в виде разложения в ряд по базисным функциям 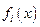 , которые удовлетворяют условиям закрепления балки (кинематические и силовые граничные условия)
, которые удовлетворяют условиям закрепления балки (кинематические и силовые граничные условия)
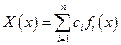 .
.
Это решение подставляют в уравнение (5.57), затем умножают полученное уравнение на произвольную базисную функцию 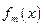 , после чего интегрируют. Повторяя эту процедуру для каждой базисной функции, приходят к алгебраической системе уравнений вида
, после чего интегрируют. Повторяя эту процедуру для каждой базисной функции, приходят к алгебраической системе уравнений вида
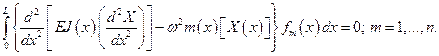 (5.58)
(5.58)
Уравнения этой системы говорят о равенстве нулю возможной работы, совершаемой упругими силами и силами инерции на перемещениях 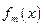 . Системе уравнений является однородной относительно неизвестных коэффициентов
. Системе уравнений является однородной относительно неизвестных коэффициентов 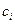 , поэтому для отыскания нетривиального решения определитель матрицы этой системы необходимо приравнять к нулю. Полученное таким путем уравнение будет содержать одну неизвестную величину – частоту свободных колебаний
, поэтому для отыскания нетривиального решения определитель матрицы этой системы необходимо приравнять к нулю. Полученное таким путем уравнение будет содержать одну неизвестную величину – частоту свободных колебаний 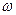 , которая может быть найдена из этого уравнения.
, которая может быть найдена из этого уравнения.
Этот метод широко применяется при проведении практических расчетов. Он позволяет найти не только собственную частоту колебаний, но и приближенное выражение для формы собственных колебаний, соответствующей этой частоте. Для этого достаточно найденное значение частоты собственных колебаний подставить в систему уравнений (5.58) и разрешить ее относительно неизвестных коэффициентов 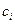 ; при этом форма собственных колебаний
; при этом форма собственных колебаний 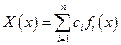 будет найдена с точностью до постоянного множителя, например
будет найдена с точностью до постоянного множителя, например 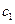 .
.
Замечание. Если базисные функции 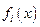 , используемые для расчета ортогональны, то процедура вычислений значительно упрощается. Это справедливо и для метода Ритца.
, используемые для расчета ортогональны, то процедура вычислений значительно упрощается. Это справедливо и для метода Ритца.
Пример 8.Шарнирно закрепленная балка переменного сечения, изображенная на рис.5.15, имеет по длине переменную изгибную жесткость
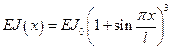
и погонную массу 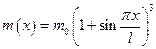

Рис.5.15
Определить методом Бубнова-Галеркина основную собственную частоту колебаний при одночленном приближении.
Решение:
Уравнение свободных колебаний балки переменного сечения записывается в виде:
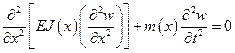 (5.59)
(5.59)
Решение представим в виде:
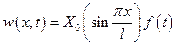 . (5.60)
. (5.60)
При данном выборе функция 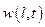 удовлетворяет краевым условиям:
удовлетворяет краевым условиям:
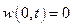 ;
;  ;
;  ;
;  .
.
После подстановки решения (5.60) в дифференциальное уравнение (5.59) умножим его на функцию 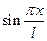 и проинтегрируем по переменной
и проинтегрируем по переменной 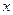 от
от 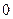 до
до 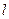 . В результате получим обыкновенное дифференциальное уравнение относительно функции
. В результате получим обыкновенное дифференциальное уравнение относительно функции 
Для определения неизвестной функции  получим дифференциальное уравнение
получим дифференциальное уравнение
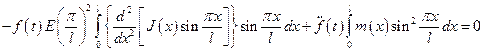 .
.
После интегрирования находим
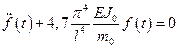 .
.
Коэффициент при втором слагаемом в этом уравнении равен квадрату основной частоты собственных колебаний
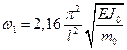 .
.
Дата добавления: 2016-02-11; просмотров: 3711;
