Уравнение колебаний струны.

Рассмотрим упругую струну, закрепленную в начальной и конечной точках (рис.5.7).

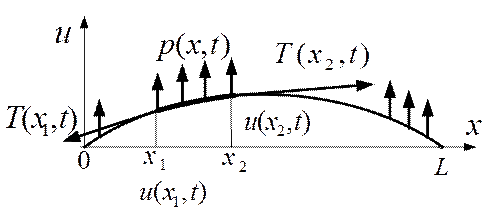
Рис.5.7.

К поверхности струны приложена поперечная изменяющаяся с течением времени распределенная нагрузка. Она является причиной возникновения вынужденных колебаний.

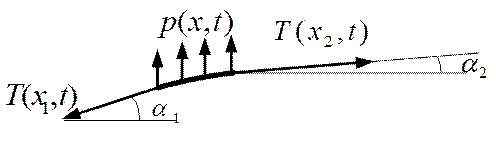
Рис.5.8.

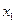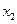Вырежем конечный элемент струны, расположенный между сечениями и (рис.5.8) и составим уравнение равновесия сил в проекции на горизонтальную ось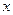

.

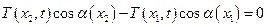Ограничимся рассмотрением малых поперечных колебаний струны 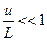, для которых можно приближенно считать

.

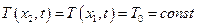Воспользуемся принципом Даламбера и составим уравнение равновесия сил в проекции на вертикальную ось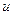

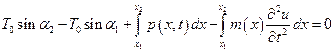, (5.29)

где 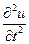- ускорение поперечного сечения струны; 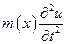- погонная сила инерции струны. Учитывая, что для малых амплитуд поперечных колебаний выполняется соотношение 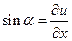, находим

.

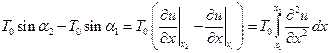Тогда уравнение поперечных колебаний струны (5.29) преобразуется к виду

.

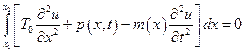Но это возможно только в том случае, если подынтегральная функция равна нулю

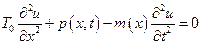. (5.30)

Если считать, что погонная масса струны постоянна 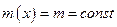, то последнее уравнение упрощается

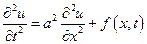(5.31)

где 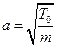; 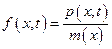. Если внешняя возмущающая нагрузка 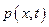отсутствует, то функция 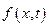будет равна нулю и уравнение вынужденных колебаний (5.31) превращается в уравнение свободных колебаний, которое называется волновым уравнением

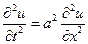. (5.32)

Свободные колебания могут возникнуть только в результате начальных возмущений, которые математически записываются в виде ненулевых начальных условий:

; .

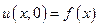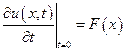Для обеспечения единственности решения поставленной задачи о свободных колебаниях, уравнение (5.32) необходимо дополнить граничными (краевыми) условиями на концах балки:

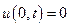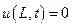; - закрепленные концы,

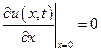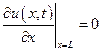; - свободные концы.