Учет внутреннего сопротивления при продольных и крутильных колебаниях стержней.

Если материал стержня не является абсолютно упругим, то при колебательном процессе необходимо учитывать внутренне трение, рассматривая материал как вязкоупругий (рис.5.6).

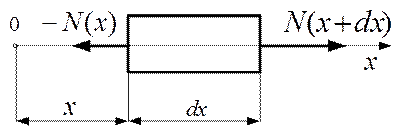
Рис.5.6.

Согласно гипотезе Фогта напряжения, возникающие в стержне, связаны с относительными деформациями соотношением [7]

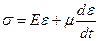, (5.18)

где 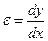- линейная относительная деформация стержня; 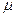- постоянный коэффициент вязкости. Согласно выражению (5.1) уравнение продольных колебаний стержня записывается в виде

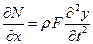, (5.19)

где 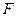- площадь поперечного сечения стержня. Согласно (5.18) продольная сила равна

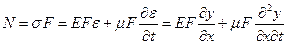. (5.20)

Для получения дифференциального уравнения колебательного движения подставим (5.20) в (5.19)

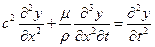, (5.21)

где 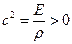. Для нахождения единственного решения необходимо, чтобы функция 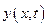удовлетворяла начальным и граничным условиям. Граничные условия, учитывающие характер закрепления концов стержня записываются в виде

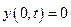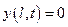, - неподвижные концы; (5.22)

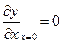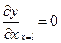, - свободные концы.

Начальные условия определяют положение и скорость движения каждого поперечного сечения стержня

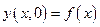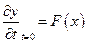и (5.23)

Для решения уравнения (5.21) воспользуемся методом Фурье. Представив решение в виде произведения двух функций

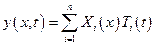. (5.24)

Здесь 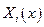- базисная функция, удовлетворяющая граничным условиям. После постановки решения (5.24) в уравнение (5.21) потребуем, чтобы каждый член ряда удовлетворял уравнению

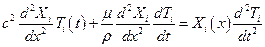. (5.25)

Если обе части этого уравнения умножить на величину

,

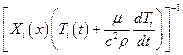то удается разделить переменные

.

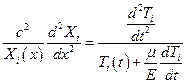Для выполнения этого уравнения каждая из его частей должна быть равна некоторой константе, например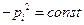

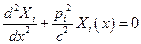; (5.26)

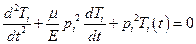(5.27)

Из уравнения (5.26) следует, что формы собственных колебаний 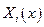не зависят от коэффициента вязкости 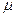, поэтому величина 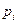полностью совпадает с собственными частотами свободных колебаний, а формы затухающих колебаний совпадают с формами свободных колебаний.

Запишем решение уравнения (5.27) в форме

.

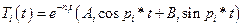где 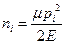, 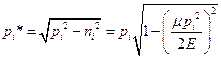. Обычно величина 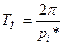называется условным периодом затухающих колебаний, так как рассматриваемый колебательный процесс строго не является периодическим. Полное решение уравнения (5.21) представляется в форме

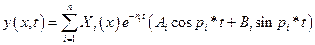, (5.28)

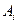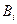где и - константы, которые находятся из начальных условий (5.21). Непосредственная подстановка решения (5.28) в эти условия приводит к алгебраической системе уравнений, из которой эти константы определяются. Чем выше номер формы собственных колебаний, тем быстрее затухает соответствующее слагаемое в решении (5.28).

Замечание. Рассмотрение процесса крутильных колебаний аналогично приведенному выше; вследствие этого формулы для описания крутильных и продольных колебаний будут обладать одинаковой структурой.