Формулировка и решение начально-краевой задачи.

Для получения единственного решения уравнения (5.5) необходимо принять во внимание два обстоятельства: во-первых, необходимо учесть характер закрепления концов стержня, а во-вторых, учесть начальные возмущения, являющиеся причиной возникновения свободных колебаний. Условия, учитывающие характер закрепления концов стержня, называются краевыми и записываются в виде

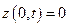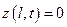, - неподвижные концы; (5.6)

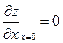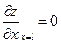, - свободные концы. (5.7)

Математическая запись начальных условий выглядит так

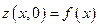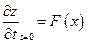и . (5.8)

Они определяют положение и скорость движения сечений стержня в момент времени 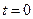. Уравнения движения (5.5), дополненное краевыми и начальными условиями, называется начально-краевой задачей. Она имеет единственное решение.

Для решения задачи воспользуемся методом Фурье. Представим решение уравнения в виде произведения двух функций 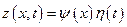и подставим в уравнение (5.5)

Умножая это уравнение на 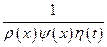приходим к выражению

.

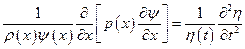Его левая часть зависит только от переменной 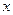, а правая часть – от . Выполнение этого равенства возможно только в том случае, если правая и левая части уравнения равны некоторой константе 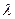, то есть

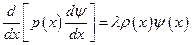и .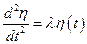

С помощью проделанного преобразования мы существенно упростили задачу, а именно перешли от уравнения в частных производных к системе двух обыкновенных дифференциальных уравнений. В результате необходимо решить две задачи:

1. «Начальная» задача

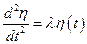; (5.9)

; .

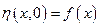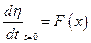2. Краевая задача

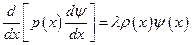; (5.10)

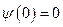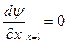; - смешанные граничные условия. (5.11)

Решение уравнения (5.9) представляется в ви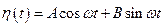де

, где 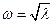(5.12)

Теорема Штурма-Лиувиля доказывает, что для краевой задачи (5.10) существует бесконечное число характеристических чисел 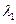,…, 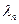( 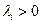), которым соответствуют формы собственных колебаний 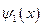,…, . Функции 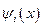являются не только решениями уравнения (5.10), но также удовлетворяют граничным условиям. Таким образом, решение начально-краевой задачи (5.5)÷(5.8), описывающей свободные колебания системы с распределенными параметрами, состоит из частных решений вида

.

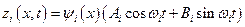В силу линейности уравнений движения, общее решение представляется как сумма частных решений

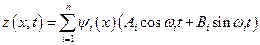. (5.13)

Начальные условия позволяют однозначно определить значения коэффициентов 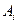и 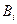. Для этого решение (5.13) необходимо подставит в начальные условия (5.8):

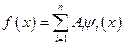; и 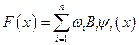. (5.14)

Таким образом, если формы собственных колебаний 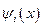образуют полную систему функций, то есть являются базисом пространства, в котором происходит движение упругой системы с распределенными параметрами, то решение можно получить за счет подбора коэффициентов 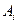и 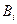так, чтобы были выполнены начальные условия (5.8).