Ортогональность форм собственных колебаний.
Формы собственных колебаний 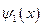 ,…,
,…,  являются решениями уравнения
являются решениями уравнения
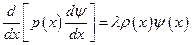 .
.
Они обращают это уравнение в тождество, поэтому справедливы равенства
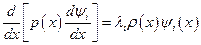 и
и 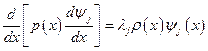 .
.
Умножая первое уравнение на 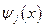 , а второе – на
, а второе – на 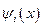 и интегрируя, найдем
и интегрируя, найдем
 ;
;
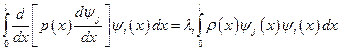 .
.
Вычитая из первого равенства второе, найдем
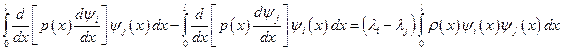 (5.15)
(5.15)
Используя интегрирование по частям и учитывая граничные условия (5.11), можно показать
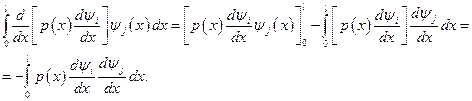
Поэтому выражение (5.15) упрощается
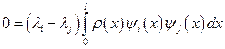 .
.
Так как собственные значения 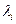 и
и 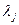 не равны, то для выполнения последнего равенства должен обращаться в нуль интеграл
не равны, то для выполнения последнего равенства должен обращаться в нуль интеграл
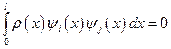 при
при 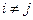 .
.
Это и есть математическая запись условия ортогональности для форм собственных колебаний.
Условие ортогональности позволяет очень просто найти постоянные коэффициенты 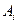 и
и 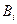 , входящие в решение (5.13). Из выражений (5.14) следует
, входящие в решение (5.13). Из выражений (5.14) следует
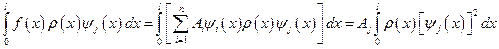 ;
;
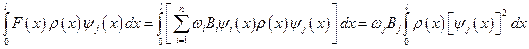 .
.
Откуда сразу находим
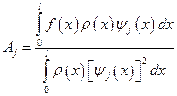 ;
; 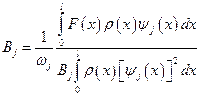 .
.
Таким образом, задачи о свободных продольных и крутильных колебаниях полностью решены.
Пример 1. Получить дифференциальное уравнение для определения собственных частот продольных колебаний ступенчатого стержня (рис.5.3) из однородного материала плотности 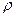 для случая, когда
для случая, когда 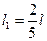 ,
, 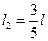 . Найти первые четыре частоты колебаний стержня.
. Найти первые четыре частоты колебаний стержня.
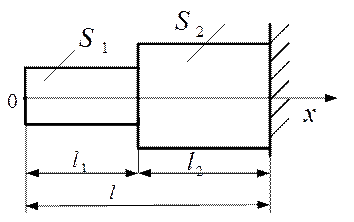
Рис.5.3.
Решение:
При постоянных 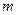 и
и 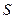 , и отсутствии внешней нагрузки
, и отсутствии внешней нагрузки 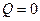 , уравнение (5.2) примет вид:
, уравнение (5.2) примет вид:
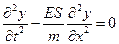 ,
,
где 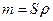 – погонная масса,
– погонная масса, 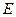 - модуль упругости 1-го рода материала. Обозначим
- модуль упругости 1-го рода материала. Обозначим
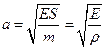
- скорость распространения возмущений в стержне, тогда будем иметь:
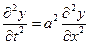 .
.
Ищем решение этого уравнение в виде:
 ,
,
где 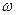 - частота колебаний. После подстановки решения в уравнение и преобразований последнего, получим
- частота колебаний. После подстановки решения в уравнение и преобразований последнего, получим
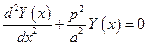 .
.
Для каждого участка стержня длиной 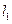 и
и  справедливо записанное уравнение. Обозначим смещение
справедливо записанное уравнение. Обозначим смещение 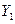 и продольную силу
и продольную силу 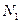 на первом участке длины
на первом участке длины 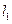 и соответственно смещение
и соответственно смещение 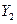 и продольную силу
и продольную силу 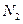 - на втором участке
- на втором участке  . Решение этого обыкновенного дифференциального уравнения для первого участка записывается в виде
. Решение этого обыкновенного дифференциального уравнения для первого участка записывается в виде
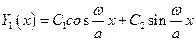 .
.
Амплитудное значение продольной силы равно
 .
.
На 1-м участке: 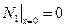 , поэтому
, поэтому 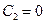 . Для амплитудного значения смещения свободного торца можно принять любое значение, например
. Для амплитудного значения смещения свободного торца можно принять любое значение, например 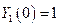 , следовательно
, следовательно
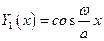 ;
; 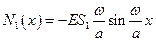 .
.
На 2-м участке решение записывается в виде:
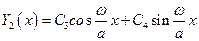 ,
,
где 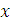 изменяется от 0 до
изменяется от 0 до 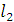 . Величина продольной силы на втором участке равна
. Величина продольной силы на втором участке равна
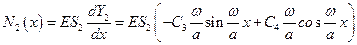 .
.
Постоянные 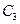 и
и 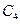 можно определить из граничных условий в сечении стыковки двух участков
можно определить из граничных условий в сечении стыковки двух участков
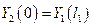 ;
;  ,
,
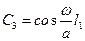 ;
; 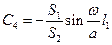 .
.
В результате решение для второго участка запишется в виде
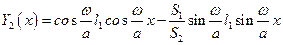 .
.
Для получения окончательного решения задачи следует удовлетворить еще одному граничному условию в сечении жесткой заделке 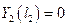 , которое сводится к решению трансцендентного уравнения относительно частоты
, которое сводится к решению трансцендентного уравнения относительно частоты 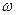 :
:
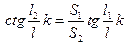 , где
, где  .
.
Решая это уравнение, например, графически, получим первые четыре корня:
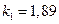 ;
; 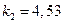 ;
; 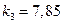 ;
; 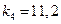 ,
,
им соответствуют частоты:
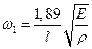 ;
; 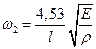 ;
; 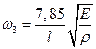 ;
; 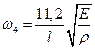 .
.
Пример 2. Определить приближенное значение амплитуд вынужденных продольных колебаний стержня, изображенного на рис.5.4, при действии гармонической продольной силы 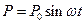 , приложенной к свободному концу стержня. Площадь поперечного сечения стержня и погонная масса изменяются по законам
, приложенной к свободному концу стержня. Площадь поперечного сечения стержня и погонная масса изменяются по законам 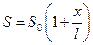 и
и 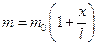 , соответственно.
, соответственно.
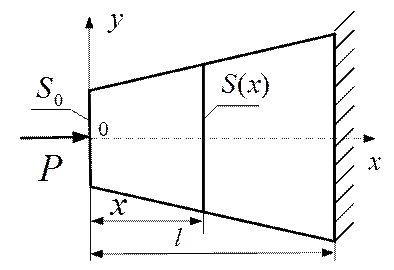
Рис.5.4.
Решение:
Решим задачу методом Бубнова - Галеркина, ограничившись одночленным приближением. Запишем уравнение (5.2) в виде:
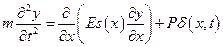 (5.16)
(5.16)
где 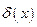 – дельта-функция. Ищем решение уравнения (5.16) при установившихся вынужденных колебаниях в виде
– дельта-функция. Ищем решение уравнения (5.16) при установившихся вынужденных колебаниях в виде 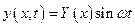 , подставив его в (5.16), получим:
, подставив его в (5.16), получим:
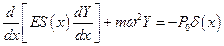 (5.17)
(5.17)
Примем 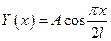 , где
, где 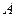 - амплитуда установившихся колебаний, соответствующая собственной форме колебаний однородного стержня. Используя метод Бубнова - Галеркина, имеем
- амплитуда установившихся колебаний, соответствующая собственной форме колебаний однородного стержня. Используя метод Бубнова - Галеркина, имеем
 .
.
Учитывая, что
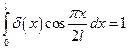
и интегрируя последнее выражение, получим:
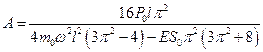 .
.
Пример 3. Вывести дифференциальные уравнения для определения собственных частот крутильных колебаний вала круглого поперечного сечения с дисками на концах (рис.5.5). Моменты инерции масс дисков 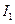 и
и 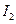 , плотность материала вала
, плотность материала вала 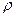 . Показать, что при
. Показать, что при 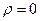 (безынерционный вал), частота колебаний дисков равна
(безынерционный вал), частота колебаний дисков равна
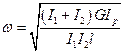

Рис.5.5.
Решение:
Из уравнения (5.4) при отсутствии внешнего момента 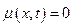 и постоянном осевом моменте инерции вала
и постоянном осевом моменте инерции вала 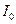 , получим:
, получим:
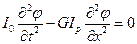 или
или 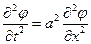 ,
,
где 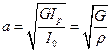 - скорость распространения волны сдвига,
- скорость распространения волны сдвига, 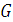 - модуль упругости 2-го рода материала,
- модуль упругости 2-го рода материала, 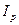 - полярный момент инерции сечения вала,
- полярный момент инерции сечения вала, 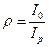 - отношение моментов инерции. Решение ищем в виде
- отношение моментов инерции. Решение ищем в виде 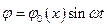 , после подстановки и преобразований получим обыкновенное дифференциальное уравнение:
, после подстановки и преобразований получим обыкновенное дифференциальное уравнение:
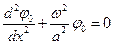 ,
,
решение которого можно записать так:
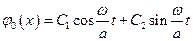 .
.
К торцам вала приложены моменты сил инерции дисков, что позволяет получить два краевых условия:
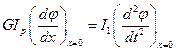 ;
;
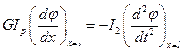 .
.
Требование выполнения этих краевых условий приводит к системе 2-х уравнений относительно 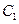 и
и 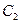 :
:
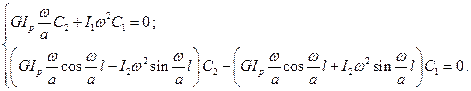
Приравнивая определитель системы к нулю, получим уравнение для определения собственных частот 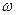
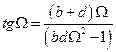 ,
,
где 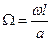 ;
; 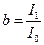 ;
; 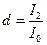 ;
; 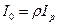 . При
. При  получаем
получаем
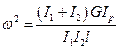 или
или 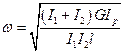 .
.
Это соответствует частоте крутильных колебаний системы, в которой два диска с моментами инерции масс 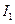 и
и 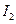 связаны безынерционным валом жесткости
связаны безынерционным валом жесткости 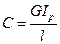 .
.
Дата добавления: 2016-02-11; просмотров: 4048;
