Крутильные колебания стержней.
Продольные колебания стержней.
Рассмотрим колебание стержня, к которому вдоль его оси приложена нагрузка 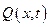 , изменяющаяся вдоль координаты
, изменяющаяся вдоль координаты 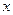 и зависящая от
и зависящая от
времени  (рис.5.1).
(рис.5.1).
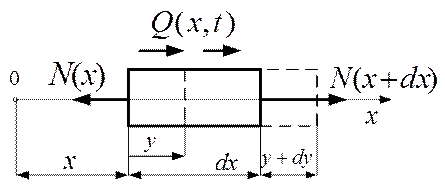
Рис.5.1.
Считая стержень упругим, вырежем из него бесконечно малый элемент 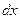 . Продольные усилия, приложенные к его торцам, определяются выражениями:
. Продольные усилия, приложенные к его торцам, определяются выражениями:
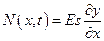 ,
, 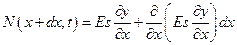 ,
,
где 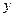 - абсолютная упругая деформация стержня в сечении
- абсолютная упругая деформация стержня в сечении 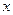 ;
;  - относительная упругая деформация;
- относительная упругая деформация;  - абсолютная упругая деформация бесконечно малого участка стержня элемента длины
- абсолютная упругая деформация бесконечно малого участка стержня элемента длины 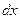 ;
; 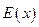 - модуль упругости материала;
- модуль упругости материала; 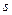 - площадь поперечного сечения (в общем случае площадь поперечного сечения
- площадь поперечного сечения (в общем случае площадь поперечного сечения 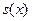 зависит от координаты
зависит от координаты 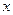 ).
).
Используя принцип Даламбера, составим уравнение равновесия сил
 (5.1)
(5.1)
где 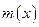 - погонная масса стержня,
- погонная масса стержня, 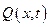 - продольная внешняя нагрузка, приложенная к поверхности стержня, а последнее слагаемое, входящее в уравнение (5.1) представляет собой силу инерции, действующую на элемент стержня
- продольная внешняя нагрузка, приложенная к поверхности стержня, а последнее слагаемое, входящее в уравнение (5.1) представляет собой силу инерции, действующую на элемент стержня 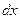 во время колебательного процесса. Обычно уравнение (5.1) принято записывать в форме:
во время колебательного процесса. Обычно уравнение (5.1) принято записывать в форме:
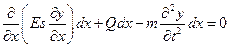 .
.
И окончательно
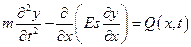 . (5.2)
. (5.2)
Крутильные колебания стержней.
Действуя, как и в случае продольных колебаний, вырежем бесконечно малой длины элемент стержня, к которому приложена распределенная нагрузка в виде скручивающего погонного момента 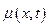 .
.
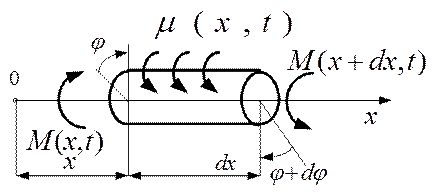
Рис.5.2.
Воспользуемся силовой схемой, представленной на рис.5.2 и с помощью принципа Даламбера составим уравнение равновесия для бесконечно малого элемента стержня
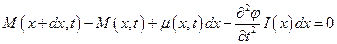 , (5.3)
, (5.3)
где 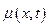 - погонный внешний момент, приложенный к поверхности стержня;
- погонный внешний момент, приложенный к поверхности стержня; 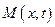 - сосредоточенный внутренний крутящий момент, приложенный к левому концу вырезанного элемента стержня;
- сосредоточенный внутренний крутящий момент, приложенный к левому концу вырезанного элемента стержня; 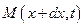 - сосредоточенный внутренний крутящий момент, приложенный к правому концу вырезанного элемента стержня;
- сосредоточенный внутренний крутящий момент, приложенный к правому концу вырезанного элемента стержня; 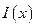 - массовый момент инерции стержня (осевой момент инерции масс);
- массовый момент инерции стержня (осевой момент инерции масс); 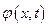 - угол поворота поперечного сечения стержня.
- угол поворота поперечного сечения стержня.
Крутящий момент на левом и правом концах элемента стержня можно представить в виде
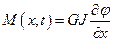 ,
, 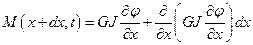 .
.
Здесь 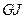 - жесткость на кручение. Тогда уравнение равновесия (5.3) запишется в виде
- жесткость на кручение. Тогда уравнение равновесия (5.3) запишется в виде
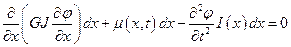 .
.
И окончательно
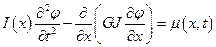 . (5.4)
. (5.4)
Замечание. Уравнения (5.2) и (5.4) являются уравнениями вынужденных колебаний. Если внешняя нагрузка, приложенная к стержню, отсутствует 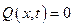 и
и 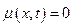 , то эти уравнения будут описывать свободные колебания стержня. При этом они имеют одинаковую математическую структуру, которая может быть представлена уравнением
, то эти уравнения будут описывать свободные колебания стержня. При этом они имеют одинаковую математическую структуру, которая может быть представлена уравнением
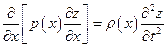 (5.5)
(5.5)
Дата добавления: 2016-02-11; просмотров: 3103;
