Вынужденные гармонические поперечные колебания балок.

Если к поверхности призматической балки приложена поперечная гармоническая возмущающая нагрузка 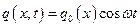, то в результате ее воздействия возникнут вынужденные колебания. Уравнения изгибных колебаний балки запишутся в форме

. (5.48)

Будем разыскивать решение этого уравнения в классе функций

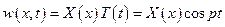. (5.49)

Непосредственная подстановка (5.49) в (5.48) дает

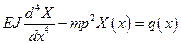(5.50)

Для определенности ограничимся рассмотрением вынужденных колебаний шарнирно закрепленной балки (рис.5.10). Представим решение уравнения (5.50) в виде разложения в ряд по формам собственных колебаний

. (5.51)

При подстановке этого решения в последнее дифференциальное уравнение (5.50), находим

.

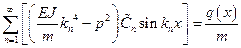Обозначим 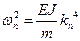, тогда умножив последнее уравнение на 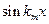и интегрируя в пределах от 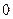до 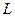, в силу ортогональности форм собственных колебаний находим

.

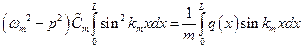Это выражение позволяет легко вычислить коэффициенты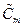

,

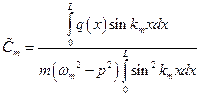которые характеризует амплитуды установившихся вынужденных колебаний, происходящие по соответствующим формам. Окончательное выражение, определяющее закон колебательного движения записывается в виде

.

Пример 6.В момент к балке постоянной жесткости внезапно прикладывается сила 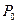, рис. 5.12. Масса единицы длины балки 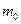Исследовать колебания балки, вызванные внезапным приложением силы 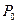и определить изменения во времени максимального нормального напряжения в сечении балки .

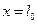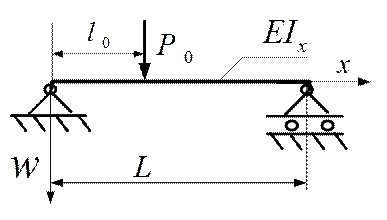
Рис.5.12.

Решение:

Дифференциальное уравнение колебаний балки примет вид:

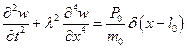(5.52)

где 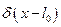- дельта-функция, обладающая следующими свойствами:

1. ;

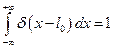2. 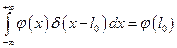, поскольку 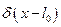отлична от нуля только на интервале , то бесконечные интегралы можно заменить на конечные ;

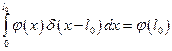3. .

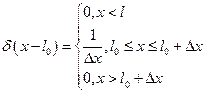Разложим дельта-функцию в ряд по собственным функциям свободных колебаний:

,

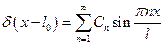где .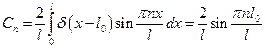

Решение дифференциального уравнения ищем в виде

.

После его подстановки в дифференциальное уравнение (5.52) находим

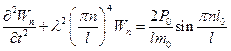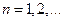, . (5.53)

При начальном условии 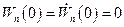решение уравнения (5.53) записывается в виде

,

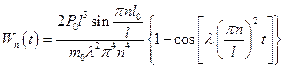а решение уравнения (5.52) как функция

.

Изгибающий момент в любом сечении балки:

.

Максимальное нормальное напряжение в сечении приложения силы:

,

где 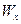- момент сопротивления выделенного сечения.