Парный критерий Стьюдента.

Ограничения: нормальное распределение изменений показателя.

Экспериментальное значение критерия рассчитывается следующим образом:

Среднее значение изменения показателя

t = -------------------------------------------------------------------------------------

Средняя ошибка среднего значения изменения показателя

Порядок расчёта:

n – численность групп;

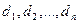- изменение показателя у конкретного больного ( );

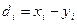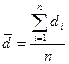- среднее значение изменения показателя;

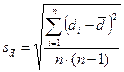- стандартная ошибка изменения показателя.

.

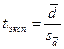Критическое значение, находится аналогично обычному критерию Стьюдента. Число степеней свободы в данном случае равно f = n-1.

Пример:

Изучали влияние курения на агрегацию тромбоцитов. У 11 добровольцев агрегация (в %) измерялась до и после выкуривания одной сигареты.

До	После	d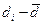
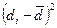
			-8,3	68,89
			-6,3	39,69
			-0,3	0,09
			1,7	2,89
			5,7	32,49
			4,7	22,09
			-6,3	39,69
			16,7	278,89
			-1,3	1,69
		-1	-11,3	127,69
			4,7	22,09
Сумма				636,19

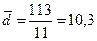
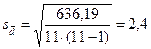
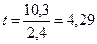
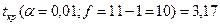
Таким образом, нулевую гипотезу об отсутствии изменения агрегации тромбоцитов при курении отвергаем с вероятностью ошибки меньше 0,01.