Множественные сравнения.
Критерий Стьюдента предназначен для сравнения двух групп. Однако на практике он широко и неправильно используется для оценки различий большего числа групп посредством попарного их сравнения. При этом вступает в силу эффект множественных сравнений. Вероятность ошибиться хотя бы в одном из нескольких сравнений составит не 0,05 (максимально допустимую вероятность ошибки), а значительно больше. В общем случае эта вероятность равна:
,
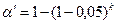где k – число сравнений.
При небольшом числе сравнений можно использовать приближённую формулу
.
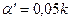Точные значения вероятности ошибки при различном числе групп приведены в следующей таблице:
| Количество групп | Количество попарных сравнений |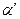 
| Множитель |
| 0,143 | 2,853 | ||
| 0,265 | 5,298 | ||
| 0,401 | 8,025 | ||
| 0,537 | 10,734 | ||
| 0,659 | 13,189 | ||
| 0,762 | 15,243 |
Таким образом, если мы проводим попарные сравнения нескольких групп и хотим с вероятностью ошибки 0,05 найти различия, надо полученную после применения критерия Стьюдента точную вероятность a умножить на соответствующий множитель (см. таблицу) или приближённо на количество попарных сравнений.
Например, мы проводим попарные сравнения четырёх групп. Таких сравнений будет 6: 1-2, 1-3, 1-4, 2-3, 2-4 и 3-4. Множитель составит 5,298. Тогда, чтоб отклонить нулевую гипотезу об отсутствии различий между сравниваемыми группами на уровне значимости 0,05, вероятность ошибки должна составить не более 0,05/5,298 = 0,0094. Можно также сравнивать экспериментальное значение с критическим, соответствующим этому значению вероятности. Это значение можно приближенно рассчитать, по соседним критическим точкам:
,
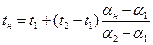где a1, a2 – значения уровня значимости; t1, t2 – критические значения соответствующие им; aн – нужный уровень значимости.
Этот же подход можно использовать при применении других критериев, предназначенных для сравнения двух групп, для множественных сравнений.
Для вычисления точного значения вероятности ошибки можно воспользоваться формулой =СТЬЮДРАСП(x; степени_свободы; хвосты) в электронных таблицах MS Excel. Здесь X – экспериментальное значение критерия Стьюдента; степени_свободы – количество степеней свободы; хвосты – 1 или 2, соответственно односторонняя или двусторонняя значимость различий будет определяться (направленная или ненаправленная гипотеза).
Пример. В задаче решенной с помощью дисперсионного анализа выяснили, что студенты, получившие разные оценки на экзамене достоверно отличаются по среднему времени нажатия. Проведем попарные сравнения групп с помощью критерия Стьюдента, для выяснения, где конкретно эти различия проявляются.
Так как всего групп четыре, то попарных сравнений будет 6 и вероятность ошибки должна составить не более 0,05/5,298 = 0,0094.
Сравниваем группы студентов получивших на экзамене «2» и «3» соответственно: n1 = 49; n2 = 72;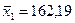 
; 
; 
; 
.
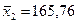Рассчитываем экспериментальное значение критерия:
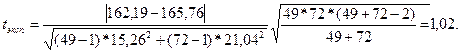
Используя электронные таблицы MS Excel определяем критическое значение критерия Стьюдента при точном значении вероятности: =СТЬЮДРАСПОБР(0,0094; 49+72-2), получаем значение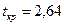 
. Таким образом, нельзя считать группы студентов сдавших экзамен на «2» и на «3» отличающихся по среднему времени нажатия.
Аналогично проведём остальные попарные сравнения.
| № | Оценка на экзамене | Первая группа сравнения | Вторая группа сравнения | tэксп | tкр | ||||
| Среднее | Среднее кв. отклонение | Численность группы | Среднее | Среднее кв. отклонение | Численность группы | ||||
| 2 и 3 | 162,19 | 15,26 | 165,76 | 21,04 | 1,02 | 2,64 | |||
| 2 и 4 | 162,19 | 15,26 | 163,10 | 15,82 | 0,33 | 2,63 | |||
| 2 и 5 | 162,19 | 15,26 | 156,55 | 14,80 | 1,97 | 2,64 | |||
| 3 и 4 | 165,76 | 21,04 | 163,10 | 15,82 | 0,93 | 2,63 | |||
| 3 и 5 | 165,76 | 21,04 | 156,55 | 14,80 | 2,89 | 2,64 | |||
| 4 и 5 | 163,10 | 15,82 | 156,55 | 14,80 | 2,59 | 2,63 |
Как видно из таблицы достоверные отличия будут наблюдаться только между сдавшими экзамен на «3» и на «5» (tэксп > tкр), остальные различия не достоверны (tэксп < tкр).
Данный способ проведения множественных сравнений при большом числе сравнений излишне строг. Для количественных данных можно воспользоваться методами, специально предназначенными для попарных сравнений, например Шеффе, Ньюмена-Кейлса, Даннета.
Выводы.
Однофакторный дисперсионный анализ применяется для сравнения количественного признака в нескольких группах. Основан на вычислении отношения межгрупповой и внутригрупповой дисперсии.
Критерий Стьюдента предназначен для сравнения количественного признака в двух группах, причём обе выборки должны быть распределены по нормальному закону и должны иметь равные генеральные дисперсии.
Экспериментальное значение критерия Стьюдента вычисляется как отношение разности выборочных средних к средней ошибке разности выборочных средних.
Критерий Фишера предназначен для сравнения выборочных дисперсий в двух группах. Может быть использован для проверки применимости критерия Стьюдента в отношении дисперсий сравниваемых выборок.
Если сравнивается несколько групп попарно, то имеет место эффект множественных сравнений, заключающийся в увеличении вероятности ошибки.
ЛИТЕРАТУРА.
Гланц С. – Глава 3,4.
Лакин Г.Ф. – с. 113-128, с. 159-179.
Реброва О.Ю. – с.104-109, с. 119-125.
Сидоренко Е. В. – с.224-240.
Вопросы для самопроверки студентов.
1. Понятие дисперсионного анализа. Ограничения метода.
2. Межгрупповая и внутригрупповая дисперсия. Критические значения. Степени свободы.
3. Область применимости критерия Стьюдента.
4. Порядок расчёта критерия Стьюдента.
5. В каких случаях применяется критерий Фишера?
6. Множественные сравнения.
Задачи.
№2, 11, 13.
Дата добавления: 2016-02-04; просмотров: 3203;