Однофакторный дисперсионный анализ.
Однофакторный дисперсионный анализ применяется для сравнения количественного признака в нескольких группах. Разработан Р.Фишером.
Ограничения:
1) каждая выборка независима от остальных выборок;
2) каждая выборка случайным образом извлечена из исследуемой совокупности;
3) совокупность нормально распределена;
4) дисперсии всех выборок можно считать равными.
Данный критерий основан на том, что в случае справедливости нулевой гипотезы оценки дисперсии генеральной совокупности, вычисленные исходя из выборочных средних и вычисленные исходя из внутригрупповых дисперсий будут приближённо равны. В противном случае межгрупповые различия будут более значительны, чем внутригрупповые. Следовательно, экспериментальное значение критерия рассчитывается как отношение этих оценок:
Дисперсия, обусловленная межгрупповыми различиями
F = ----------------------------------------------------------------------------------------
Дисперсия, обусловленная внутригрупповыми различиями
Критическое значение будет показывать, до какой величины значение отношения дисперсий будет проявлением случайных межгрупповых различий при заданной вероятности ошибки.
Исходные данные для расчёта:
k – количество сравниваемых групп;
ni – численность i-ой группы;
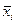 – среднее в i-ой группе;
– среднее в i-ой группе;
si – среднее квадратическое отклонение в i-ой группе.
Порядок расчёта:
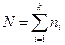 ;
;
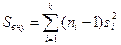 ;
; 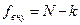 ;
; 
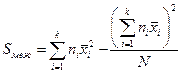 ;
; 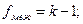
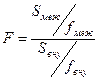 .
.
Полученное значение Fэксп сравнивают со значением критической точки Fкр (α; fмеж ; fвну) распределения Фишера (см. приложение), где α– уровень значимости.
Критическое значение можно также определить в электронной таблице Microsoft Excel используя функцию FРАСПОБР(α, fмеж , fвну).
Если Fэксп < Fкр, то нулевую гипотезу с принятой вероятностью считают согласующейся с результатами наблюдений (различия в выборочных средних считаются незначительными).
Если Fэксп > Fкр, то нулевую гипотезу отвергают в пользу конкурирующей, и различия в выборочных средних считают проявлением различия генеральных средних.
Пример: при изучении адаптации студентов к учебной деятельности за один день до экзамена проводился ряд психофизиологических тестов, в частности теппинг-тест, в котором в течение минуты нужно как можно быстрее нажимать на клавишу. По этому тесту оценивали силу нервной системы испытуемого, основным показателем его являлось среднее время нажатия. В зависимости от результатов экзамена студенты были разделены на следующие группы (M±m = 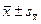 ):
):
| Экзаменационная оценка | ||||
| «2» (n=49) | «3» (n=72) | «4» (n=93) | «5» (n=62) | |
| Среднее время нажатия, мс | 162,19±2,18 | 165,76±2,48 | 163,10±1,64 | 156,55±1,88 |
Проверить гипотезу о равенстве среднего времени нажатия в группах студентов, отличающихся по экзаменационной оценке.
Итак, в нашем случае:
k = 4;
n1 = 49; n2 = 72; n3 = 93; n4 = 62; N = 49 + 72 + 93 + 62 = 276;
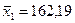 ;
; 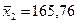 ;
; 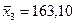 ;
; 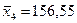 ;
;
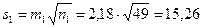 ;
; 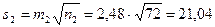 ;
;
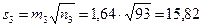 ;
; 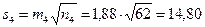 .
.
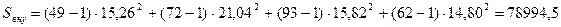
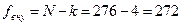 ;
; 
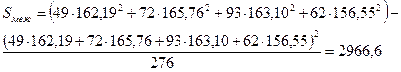 ;
;
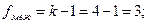
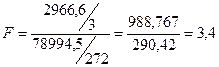
Fкр (0,05; 272; 3) = 2,64
Экспериментальное значение критерия Фишера больше критического (3,4>2,64), таким образом, при вероятности ошибки меньше 0,05 нулевую гипотезу о равенстве среднего времени нажатия в сравниваемых группах можно отвергнуть, т.е. среднее время нажатия достоверно отличается у студентов, получивших разную оценку на экзамене.
Дата добавления: 2016-02-04; просмотров: 681;
