Критерий Стьюдента.

Область применимости:

1) сравнение количественного признака в двух группах;

2) обе выборки распределены по нормальному закону;

3) есть основания считать генеральные дисперсии равными.

Экспериментальное значение критерия рассчитывается следующим образом:

Разность выборочных средних

t = ----------------------------------------------------------------------

Средняя ошибка разности выборочных средних

По результатам выборочных наблюдений (объем выборок величин X₁ и X₂ соответственно n₁ и n₂) находят выборочные средние 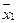, , 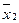оценки дисперсии 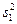, 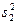и вычисляют экспериментальное значение критерия t_эксп по формуле:

.

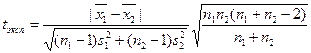Если численности сравниваемых групп равны, то можно вычислить по более простой формуле:

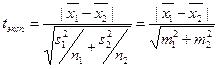, где m₁, m₂ – соответствующие средние ошибки средних.

Полученное значение t_эксп сравнивают со значением критической точки t_кр (α; f) распределения Стьюдента (см. приложение), где f = n₁ + n₂ – 2 – число степеней свободы; α– уровень значимости.

Критическое значение можно также определить в электронной таблице Microsoft Excel используя функцию =СТЬЮДРАСПОБР(α, f), где вместо α надо ввести уровень значимости, а вместо f – число степеней свободы.

Если t_эксп < t_кр, то нулевую гипотезу с принятой вероятностью считают согласующейся с результатами наблюдений (различия в выборочных средних считаются незначительными).

Если t_эксп > t_кр, то нулевую гипотезу отвергают в пользу альтернативной, и различия в выборочных средних считают проявлением различия генеральных средних.

Пример. Измерения пульса 10 больных, проведенные после некоторой процедуры, и 12 больных контрольной группы дали следующие результаты: для I группы 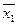= 70 уд/мин, для II группы 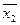= 68 уд/мин; оценки дисперсий соответственно равны: 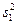= 9 (уд/мин)², и 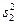= 4 (уд/мин)². При уровне значимости α = 0,05 определить, значимо ли различаются средние значения пульса у больных этих двух групп.

В качестве нулевой принимаем гипотезу о равенстве средних значений пульса в генеральных совокупностях больных, принявших процедуру, и больных, ее не принявших, считая, что распределение значений пульса подчиняется, в целом, закону нормального распределения.

Определяем экспериментальное значение критерия t_эксп:

t_эксп =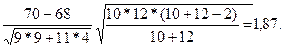

Из приложения находим t_кр (0,05; 20) = 2,086.

Так как t_эксп < t_кр, то нулевую гипотезу следует считать согласующейся с результатами наблюдений: различия в средних значениях пульса не является статистически значимым и может быть обусловлено случайными причинами, а не влиянием процедуры.

В электронных таблицах Microsoft Excel возможно сравнение выборок по критерию Стьюдента непосредственно по исходным данным. Для этого используется функция: = ТТЕСТ(массив1; массив2; хвосты; тип).

Здесь массив1 – исходные данные для первой группы;

массив2 – исходные данные для второй группы;

хвосты – 1 или 2, соответственно односторонняя или двусторонняя значимость различий будет определяться (направленная или ненаправленная гипотеза);

тип – 1 - парный критерий Стьюдента; 2 – критерий Стьюдента для равных дисперсий в сравниваемых группах; 3 – критерий Стьюдента для неравных дисперсий в сравниваемых группах.

Результатом будет являться вероятность ошибки первого рода. Если она не превышает допустимую (0,05; 0,01; 0,001), то нулевая гипотеза о равенстве средних отвергается.

Описанный выше вариант критерия Стьюдента предназначен именно для одинаковых дисперсий. Расчёт для неравных дисперсий более сложен. Проверить, можно ли считать дисперсии в группах одинаковыми можно по критерию Фишера (см. далее). В электронных таблицах это функция: ФТЕСТ(массив1, массив2). Результат вероятность ошибки первого рода при проверке гипотезы о равенстве дисперсий. Если она больше 0,05, то дисперсии нельзя считать равными и следует воспользоваться для сравнения средних вариантом критерия Стьюдента для неравных дисперсий.

Критерий Фишера.

Одним из необходимых условий применения критерия Стьюдента является равенство дисперсий изучаемых величин. В ряде случаев действительно могут быть основания для подобного предложения, но, строго говоря, в каждом конкретном случае выполнение этого условия нуждается в проверке. Такая проверка основана на использовании распределения Фишера и заключается в следующем.

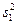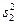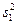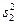Пусть по результатам наблюдений двух нормально распределенных случайных величин X₁ и X₂ (объемы выборок n₁ и n₂ соответственно) найдены оценки дисперсии и . Как правило, эти оценки различаются по величине независимо от равенства соответствующих дисперсий в генеральной совокупности. Для проверки значимости различия между и выдвигают нулевую гипотезу о равенстве генеральных дисперсий ( 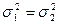), а в качестве альтернативной – гипотезу о их неравенстве ( 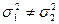). Задают также уровень значимости a, с которым проводится проверка. Далее вычисляют экспериментальное значения критерия, определяемого как отношение большей из оценок дисперсий к меньшей:

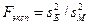
По таблице критических значений распределения Фишера (см. приложение, те же таблицы, что и для дисперсионного анализа) при уровне значимости, равном половине заданного уровня a, находят критическое значение F_кр(a/2, f₁, f₂). Здесь степени свободы: f₁= (n_Б - 1) есть уменьшенный на единицу объем выборки с большой дисперсией, f₂ = (n_М – 1) - уменьшенный на единицу объем выборки с меньшей дисперсией.

Если F_эксп < F_кр, нулевую гипотезу считают согласующейся с результатами наблюдений.

Если F_эксп > F_кр, эту гипотезу отвергают в пользу альтернативной.

В некоторых случаях в качестве конкурирующей выдвигают гипотезу о превышении одной из генеральных дисперсий значения другой (ненаправленная гипотеза). Например, если оценка дисперсии 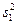оказалась большей, чем 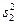, в качестве альтернативной выдвигают гипотезу 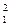σ > σ 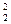. Тогда при проверке гипотезы, используют критическое значение распределения Фишера, соответствующее полной величине уровня значимости a: F_кр (a, n₁ -1, n₂ - 1).

Пример. При уровне значимости a = 0,05 проверить гипотезу о равенстве генеральных дисперсий по результатам, приведенным в предыдущем примере.

Решение. 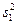= 9 > 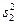= 4, поэтому, подставив численные значения в формулу, получим F_эксп = 9/4 = 2,25.

По таблице критических значений распределения Фишера (см. приложение) находим F_кр (0,05/2 = 0,025; 9; 11) = 3,588.

Поскольку F_эксп < F_кр, гипотезу о равенстве генеральных дисперсий можно считать согласующейся с результатами наблюдений.