Описание качественных и порядковых признаков.
Для этих признаков вычисление среднего не имеет смысла, даже если мы закодируем значения этих признаков в виде цифровых значений. В этом состоит распространённая ошибка в описании таких данных. Например, признак оценивается в баллах, и вычисляют средний балл, но если нельзя сказать во сколько раз, например балл 3 больше, чем балл 1, то этот признак порядковый и среднее вычислять нельзя.
Для порядковой шкалы значения можно упорядочить по возрастанию, поэтому для неё возможно определение медианы и квартилей. Это определение будет аналогично определению для количественных признаков.
Для качественных признаком единственно возможным описанием является вычисление долей, т.е. какую долю составляет количество элементов совокупности, имеющих то или иное возможное значение от общего числа элементов. Например, пусть у нас группа из 100 человек включает 40 мужчин и 60 женщин. Тогда для качественного признака пол значения долей будут: 0,4 для мужского пола и 0,6 для женского. Долю часто выражают в процентах.
Для доли можно рассчитать среднее квадратическое отклонение и среднюю ошибку доли. Среднее квадратическое отклонение будет однозначно определяться самой долей:
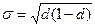 ,
,
где d – доля соответствующего значения.
Например, для вышеприведённого примера: 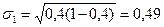 ;
; 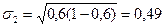 . Как видим, для дихотомического признака (только два возможных значения) средние квадратические отклонения долей будут равны.
. Как видим, для дихотомического признака (только два возможных значения) средние квадратические отклонения долей будут равны.
Средняя ошибка доли будет рассчитываться аналогично средней ошибке среднего, как отношение среднего квадратического отклонения к квадратному корню из объёма выборки. Это можно заменить на квадратный корень из отношения дисперсии к объёму выборки:
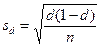 ,
,
где d – доля соответствующего значения, n – объём выборки (численность группы). В нашем примере средняя ошибка доли составит 0,49/10 = 0,049 и для мужчин и для женщин.
Смысл средней ошибки доли такой же, как и для средней ошибки среднего арифметического: средняя ошибка доли является мерой точности, с которой выборочная доля является оценкой истинной доли по всей совокупности; истинная доля по совокупности примерно в 95% случаев лежит в пределах 2 средних ошибок доли.
Таким образом, по рассмотренному примеру можно сказать, что доля мужчин и женщин во всей совокупности находится в пределах (0,4±0,098) и (0,6±0,098) соответственно с вероятностью 95%.
Порядковые признаки также можно описать с помощью долей их возможных значений.
При вычислении в электронных таблицах Microsoft Excel непосредственно по исходным данным можно использовать следующие функции:
=СРЗНАЧ(массив) – для расчёта среднего арифметического;
=СТАНДАРТОТКЛОН(массив) – для расчёта среднего квадратического отклонения;
= СТАНДАРТОТКЛОН(массив)/КОРЕНЬ(СЧЕТ(массив)) – для расчёта средней ошибки среднего;
=КВАРТИЛЬ(массив; часть) – для расчёта медианы и квартилей.
=ПЕРСЕНТИЛЬ(массив;k) – для расчёта любых процентилей, можно использовать для расчёта медианы и квартилей.
Здесь массив – это диапазон ячеек, где находятся исходные данные, например Е2:Е33;
часть – значение, определяющее номер квартиля: 1 – первый квартиль, 2 – второй квартиль (медиана), 3 – третий квартиль;
k – значение от 0 до 1, определяющие процентиль, например, для медианы это будет 0,5, для третьего квартиля 0,75.
Примеры.
В исследовании когнитивных функций у 32 детей были получены следующие результаты:
| Время выполнения 1-го задания по табл. Шульте, с | ||||||||||||||||
| Количество |
Грубые ошибки при выполнении этого задания наблюдались у 8 детей.
| Оценка зрительной памяти, балл | (значительно снижена) | (умеренно снижена) | 6 (норма) |
| Количество |
Итак, у нас имеется три признака, описывающие когнитивные функции у обследованных детей: время выполнения первого задания по таблице Шульте (количественный), наличие ошибок при выполнении этого задания (качественный) и оценка зрительной памяти (порядковый, поскольку мы не можем сказать во сколько раз зрительная память например в норме лучше, чем при умеренном снижении).
Рассчитаем среднее и среднее квадратическое отклонение. Исходными данными у нас является дискретный ряд распределения, поэтому можно для расчёта среднего и среднего квадратического отклонения использовать следующие формулы (заменяя сумму одинаковых чисел произведением этого числа на сколько раз оно встречается):
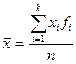 , где k – число столбцов в ряде распределения, f – частота (сколько раз встречается то или иное значение);
, где k – число столбцов в ряде распределения, f – частота (сколько раз встречается то или иное значение);
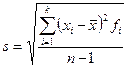 .
.
Вычисления удобно проводить в таблице:
| xi | S | ||||||||||||||||
| fi | |||||||||||||||||
| xifi | |||||||||||||||||
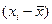
| -33,4 | -28,4 | -23,4 | -18,4 | -13,4 | -8,4 | -3,4 | 1,6 | 6,6 | 11,6 | 16,6 | 21,6 | 26,6 | 31,6 | 36,6 | 46,6 | |
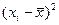
| 1115,6 | 806,6 | 547,6 | 338,6 | 179,6 | 70,56 | 11,6 | 2,6 | 43,6 | 134,6 | 275,6 | 466,6 | 707,6 | 998,6 | 1339,6 | 2171,6 | |
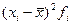
| 1115,6 | 806,6 | 1642,7 | 338,6 | 718,2 | 141,1 | 57,8 | 7,68 | 130,7 | 403,7 | 275,6 | 466,6 | 707,6 | 998,6 | 1339,6 | 2171,6 | 11321, |
Среднее 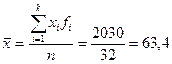 .
.
Среднее квадратическое отклонение 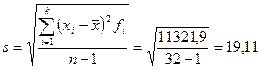 .
.
Найдём медиану и квартили. Всего 32 значения, значит, половину будет составлять 16 значений. Медиану и квартили можно определить и по дискретному ряду, а не только по упорядоченному. Считаем частоты и смотрим где накапливается частота равная половине ряда по значению – 16. Это будет число 60 (суммируем частоты: 1+1+3+1+4+2+5 = 17). Таким образом, в исходном ряду 16-ое и 17-ое число равно 60, а значит, медиана равна Me = (60+60)/2 = 60 с. Аналогично находим первый квартиль, это значение между 8-м и 9-м в ряду: Q1 = (50+50)/2 = 50. И третий квартиль, это значение между 24-м и 25-м числом: Q3 = (75 + 75)/2 = 75.
Медиана не совпадает со средним, это уже говорит о несимметричности распределения. Сравним также квартили и отклонения от среднего:
| Квартили | Q1 | Q2 | Q3 | |||
| Отклонения от среднего | m-0,7s | 50,02 | m | 63,4 | m+0,7s | 76,77 |
Как видим, первый и третий квартиль не сильно отличаются от соответствующих отклонений, т.е. асимметричность ряда небольшая и можно использовать для описания ряда среднее и среднее квадратическое отклонение, наряду с медианой и квартилями.
Качественный признак имеет два возможных значения: есть грубая ошибка при выполнении задания; нет грубой ошибки при выполнении задания. Грубые ошибки наблюдались у 8 детей, поэтому доля первого значения d1 = 8/32 = 0,25, доля второго значения d2 = (32-8)/32 = 0,75. Средние ошибки долей равны 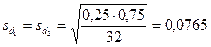 .
.
Для порядкового признака найдём медиану и квартили, а также доли отдельных значений.
| Оценка зрительной памяти, балл | 4 (значительно снижена) | 5 (умеренно снижена) | 6 (норма) |
| Количество |
Медианой является Me = 5, так как в исходном ряду 16-ое и 17-ое значение равно 5. Первый квартиль – это значение между 8-м и 9-м в ряду: Q1 = (5+5)/2 = 5. Третий квартиль – это значение между 24-м и 25-м числом: Q3 = (6+6)/2 = 6.
При небольшом числе возможных значений при описании порядковых признаков предпочтительнее использовать доли.
Значительное снижение зрительной памяти (4 балла) наблюдалось у 3-х детей, поэтому доля этого значения d1 = 3/32 = 0,094. Средняя ошибка доли 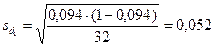 . Умеренное снижение зрительной памяти (5 баллов) наблюдалось у 19-и детей, поэтому доля этого значения d2 = 19/32 = 0,594. Средняя ошибка доли
. Умеренное снижение зрительной памяти (5 баллов) наблюдалось у 19-и детей, поэтому доля этого значения d2 = 19/32 = 0,594. Средняя ошибка доли 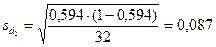 . Зрительная память в норме (6 баллов) наблюдалась у 10 детей, поэтому доля этого значения d3 = 10/32 = 0,312. Средняя ошибка доли
. Зрительная память в норме (6 баллов) наблюдалась у 10 детей, поэтому доля этого значения d3 = 10/32 = 0,312. Средняя ошибка доли 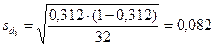 .
.
Представим результаты в итоговой таблице:
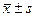
| Q1 | Me | Q3 | d±sd | ||||
| Время выполнения 1-го задания по таблице Шульте, с | 63,4±19,11 | |||||||
| Наличие грубых ошибок при выполнении 1-го задания | есть | нет | ||||||
| 0,25± 0,0765 | 0,75± 0,0765 | |||||||
| Оценка зрительной памяти, балл | ||||||||
| 0,094± 0,052 | 0,594± 0,087 | 0,312± 0,082 | ||||||
Основные понятия проверки статистических гипотез.
Как правило, основная задача проводимого научного эксперимента в медицине состоит в доказательстве различий между экспериментальной группой и контрольной по какому-либо показателю. Например, если мы хотим доказать, что этот показатель может являться диагностическим признаком данного заболевания, то сравниваем группу больных данным заболеванием с группой практически здоровых. Или мы разработали новый метод лечения данного заболевания, тогда для доказательства его эффективности по сравнению с имеющимися, мы сравниваем группы больных леченных известным методом и новым методом. Различия этих групп по показателям, характеризующим эффективность лечения будет говорить о предпочтительности нового метода. Для получения такого рода выводов в статистике необходимо проверить гипотезу о равенстве параметров двух или нескольких распределений.
Во многих случаях для решения основной задачи приходится решить ряд вспомогательных задач. Например, многие методы проверки гипотез чувствительны к виду распределения признака. Для проверки соответствует ли закон распределения признака конкретному виду (назовем его А), выдвигают гипотезу: генеральная совокупность распределена по закону А.
Гипотеза, т.е. предположение, может быть каким угодно и о чём угодно. Но выше приведенные примеры гипотез называются статистическими гипотезами.
Статистическая гипотеза – гипотеза о виде неизвестного распределения, или о соотношении параметров известных распределений.
Например, статистическими будут гипотезы:
1) совокупность распределена по равномерному закону;
2) дисперсии двух нормально распределенных совокупностей равны между собой;
3) средние арифметические двух нормально распределенных совокупностей равны между собой.
Бывают задачи, когда мы хотим доказать не значимость различий, то есть подтвердить нулевую гипотезу. Например, нам нужно убедиться, что экспериментальная и контрольная выборки не различаются между собой по каким-то значительным характеристикам. Однако чаще все-таки требуется доказать значимость отличий, т.к. они более информативны, поэтому наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза в ходе статистической проверки будет отвергнута, то имеет место противоречащая ей гипотеза. По этой причине целесообразно различать эти гипотезы.
Нулевая гипотеза – это гипотеза об отсутствии различий.
Она обозначается как Н0 и называется нулевой потому, что говорит об отсутствии различий между сопоставляемыми значениями признаков X1 и X2, т.е. разница между ними будет равна 0: Х1 – Х2 = 0.
Нулевая гипотеза – это то, что мы хотим принять, если перед нами стоит задача доказать случайность различий, или опровергнуть, если перед нами стоит задача доказать значимость различий.
Альтернативная (конкурирующая) гипотеза – это гипотеза противоположная нулевой, т.е. о значимости различий. Она обозначается как Н1.
Чаще всего хотят доказать именно значимость различий, поэтому её иногда называют экспериментальной гипотезой.
Нулевая и альтернативная гипотезы могут быть направленными и ненаправленными. Если мы хотим доказать, что в группе А значение показателя больше (меньше), чем в группе Б, то нам необходимо сформулировать направленные гипотезы. Если мы хотим доказать, что группы А и Б просто различаются по данному показателю (не учитывая в какой группе больше, в какой меньше), то формулируются ненаправленные гипотезы.
| Направленные гипотезы Н0: Х1 не превышает Х2 Н1: Х1 превышает Х2 | Ненаправленные гипотезы Н0: Х1 не отличается от Х2 Н1: Х1 отличается от Х2 |
Направленные гипотезы доказать проще, потому что отслеживается изменение признака только в одну сторону, а не в обе. В статистических таблицах, как правило, указывается, для какого случая приведены значения: двусторонняя значимость, т.е. для ненаправленной гипотезы, или односторонняя значимость, для направленной гипотезы. Последняя будет в два раза меньше.
Естественно, любое предположение, в том числе и статистическое, может оказаться неверным, т.е. могут быть допущены ошибки.
Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.
Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.
Такое разделение ошибок не случайно, оно связано с их влиянием на последующее применение результатов эксперимента. Ошибка первого рода состоит в том, что мы отвергли верную нулевую гипотезу, т.е. различий на самом деле нет, а мы их доказали. Например, если мы доказываем эффективность какого-либо препарата при лечении заболевания, эта ошибка представляет собой заключение об эффективности препарата, хотя он на самом деле не эффективен.
Ошибка второго рода состоит в том, что мы приняли нулевую гипотезу, а она неверна, т.е. мы не смогли доказать различия, хотя они на самом деле есть. Препарат на самом деле эффективен, а мы даём заключение о его неэффективности. Понятно, что вторая ошибка менее опасна, чем первая. Препарат не будут применять, хотя он эффективен. Но гораздо хуже применять неэффективный препарат. Поэтому очень часто учитывают только ошибку первого рода и именно её вероятность хотят сделать как можно меньше.
Вероятность совершить ошибку первого рода называют уровнем значимости. Будем обозначать величину вероятности ошибки первого рода a.
Вероятность не совершить ошибку первого рода, т. е. принять верную гипотезу, называют доверительной вероятностью. Она равна 1 - a.
Вероятность ошибки второго рода будем обозначать b.
Вероятность не совершить ошибку второго рода, т.е. отвергнуть неверную гипотезу (доказать различия, если они действительно есть) называют мощностью критерия, она будет равна 1 - b.
Естественно, нужно стремиться к тому, чтобы все правильные гипотезы были приняты, а неверные отвергнуты, т.е. чтобы вероятности ошибок первого и второго рода a и b были как можно меньше.
Однако, при заданном объеме выборки это невозможно, чем меньше взять уровень значимости a, тем больше будет b (ниже мощность критерия).
Единственный способ одновременного уменьшения a и b состоит в увеличении объема выборок.
Проверка гипотез осуществляется с помощью статистической оценки различий или, иначе, статистических критериев.
Статистический критерий – это случайная величина К, которая служит для проверки нулевой гипотезы.
Статистический критерий – это правило, обеспечивающее надежность принятия истинной и отклонение ложной гипотезы с определенной вероятностью.
Статистический критерий – это также метод расчета числа К и само это число.
После выбора определенного критерия, множество всех его значений разбиваются на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другое – при которых она принимается.
Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.
Областью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают.
Рассматриваемые нами критерии являются одномерными, т.е. все возможные значения случайной величины принадлежат некоторому интервалу. Поэтому критическая область и область принятия гипотезы также являются интервалами и существуют точки, которые их разделяют.
Критическими точками Ккрит называют точки, отделяющие критическую область от области принятия гипотезы.
Для проверки гипотезы по данным выборок вычисляют частные значения входящих в критерий величин, и таким образом получают частное (экспериментальное, эмпирическое) значение критерия Кэксп.
Основной принцип проверки статистических гипотез.
Если наблюдаемое (экспериментальное) значение критерия принадлежит критической области, т.е. Кэксп >= Ккрит, то гипотезу отвергают, если наблюдаемое (экспериментальное) значение критерия принадлежит области принятия критерия, т.е. Кэксп < Ккрит, то гипотезу принимают.
Исторически сложилось так, что в лабораторных и научных исследованиях принято низшим уровнем статистической значимости считать 5% - ый уровень (a = 0,05), достаточным – 1% - ый (a = 0,01) и высшим 0,1% - ый (a = 0,001). Таким образом, пока статистический уровень значимости не достигнет a = 0,05, мы еще не имеем права отклонить нулевую гипотезу.
Дата добавления: 2016-02-04; просмотров: 2448;
