Описание количественных признаков.
Если значения интересующего нас признака у большинства объектов близки к их среднему и с равной вероятностью отклоняются от него в большую или меньшую сторону, лучшими характеристиками совокупности будут само среднее значение и среднее квадратическое отклонение. Напротив, когда значения признака распределены несимметрично относительно среднего, совокупность лучше описать с помощью медианы и квартилей.
Раз существует множество похожих распределений, значит, для характеристики одного из них достаточно указать, чем оно отличается от других, ему подобных, то есть всю собранную информацию мы можем свести к нескольким числам, которые называются параметрами распределения. Это среднее значение и среднее квадратическое отклонение (в переводной литературе оно называется стандартное отклонение (standard deviation)).
Среднее.
Характеристика положения распределения на числовой оси называется средним. Среднее по совокупности обозначают 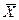 или греческой буквой m (читается «мю») и вычисляют по формуле:
или греческой буквой m (читается «мю») и вычисляют по формуле:
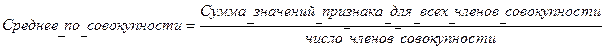

Эквивалентное математическое выражение имеет вид: 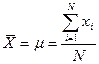 ,
,
где xi – значение признака, N – число членов совокупности. Большая греческая буква S (читается «сигма») обозначает сумму, т.е. 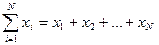 .
.
Дата добавления: 2016-02-04; просмотров: 732;
