Насколько точны выборочные оценки.

Выборочное среднее и выборочное среднее квадратическое отклонение есть оценки среднего и среднего квадратического отклонения для совокупности, вычисленные по случайной выборке. Понятно, что разные вы­борки дадут разные оценки. Для характеристики точности выбо­рочных оценок используют среднюю ошибку. Среднюю ошибку можно подсчитать для любого показателя, но сейчас мы остановимся на средней ошибке среднего – она позволяет оценить точность, с которой выборочное среднее характеризует значение среднего по всей совокупности.

Проведём такой мысленный эксперимент. Пусть у нас имеется совокупность объёма N, параметры которой мы оцениваем по выборке объёма n. Будем брать все возможные выборки объёма n из совокупности, каждый раз вычисляя среднее и среднее квадратическое отклонение. Таких выборок будет очень и очень много. Например, если мы берём выборки по 10 элементов из совокупности в 200 элементов, то общее число всех возможных выборок будет порядка 10¹⁶.

Опишем распределение полученных выборочных средних. Можно доказать, что если переменная представляет собой сумму большого числа независимых пере­менных, то ее распределение стремится к нормальному, какими бы ни были распределения переменных, образующих сумму. Так как выборочное среднее определяется именно такой суммой, его распределение стремится к нормальному, причем, чем больше объем выборок, тем точнее приближение. (Если выборки при­надлежат совокупности с нормальным распределением, распре­деление выборочных средних будет нормальным независимо от объема выборок.)

Поскольку распределение всевозможных выборочных средних нормальное, его можно описать с помощью среднего и среднего квадратического отклонения.

Так как рассматриваемое среднее значение есть среднее величин, которые сами являются средними значения­ми, обозначим его 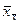. Аналогично, среднее квадратическое отклонение выборочных средних обозначим .

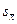Среднее выборочных средних 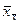совпадет со средним по совокупности m. Действительно, так как мы провели исследования всех возможных выборок, то каждый из элементов совокупности будет вы­бран равное число раз.

Подобно тому, как среднее квадратическое отклонение выборки s служит оценкой изменчивости роста марсиан, 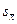является оценкой изменчивости значений средних для множества выбо­рок такого же объёма. Таким образом, величина 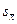служит мерой точности, с которой выборочное среднее 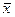является оцен­кой среднего по совокупности m. Поэтому 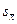носит название средней ошибки среднего.

Чем больше выборка, тем точнее оценка среднего и тем мень­ше его средняя ошибка. Чем больше изменчивость исходной совокупности, тем больше изменчивость выборочных средних; поэтому средняя ошибка среднего возрастает с увеличением среднего квадратического отклонения совокупности.

Истинная средняя ошибка среднего по выборкам объе­мом n, извлеченным из совокупности, имеющей среднее квадратическое отклонение s, равна: .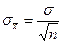

Собственно средняя ошибка – это наилучшая оценка ве­личины 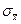по одной выборке: 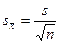, где s – выборочное среднее квадратическое отклонение. Для обозначения средней ошибки среднего также часто применяется m.

Так как возможные значения выборочного среднего стремят­ся к нормальному распределению, истинное среднее по сово­купности примерно в 95% случаев лежит в пределах 2 средних ошибок выборочного среднего. На этом основано определение доверительных интервалов, что будет рассмотрено в соответствующей теме.

Как уже говорилось, распределение выборочных средних при­ближенно всегда следует нормальному распределению незави­симо от распределения совокупности, из которой извлечены вы­борки. В этом и состоит суть утверждения, называемого цен­тральной предельной теоремой. Эта теорема гласит следующее:

· Выборочные средние имеют приближенно нормальное распределение независимо от распределения исходной совокупности, из которой были извлечены выборки.

· Среднее значение всех возможных выборочных средних рав­но среднему исходной совокупности.

· Среднее квадратическое отклонение всех возможных средних по выбор­кам данного объема, называемое средней ошибкой сред­него, зависит как от среднего квадратического отклонения совокупности, так и от объема выборки.

С увеличением объёма выборки, вы­борочное среднее 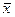и среднее квадратическое отклонение s дают все более точные оценки среднего m и среднего квадратического отклонения sпо сово­купности. Увеличение точности оценки среднего отражается в уменьшении средней ошибки среднего 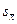. В отличие от среднего квадратического отклонения средняя ошибка среднего ничего не говорит о раз­бросе данных – она лишь показывает точность выборочной оцен­ки среднего.

Хотя разница между средним квадратическим отклонением и средней ошибкой среднего совершенно очевидна, их часто путают. Большинство исследователей приводят в публикациях значение средней ошибки среднего, которая заведомо меньше среднего квадратического отклонения (в корень из объёма выборки раз). Авторам кажется, что в таком виде их дан­ные внушают больше доверия. Может быть, так оно и есть, одна­ко беда в том, что средняя ошибка среднего измеряет имен­но точность оценки среднего, но никак не разброс данных, кото­рый и интересен читателю. Описывая совокупность, всегда нужно приводить значение среднего квадратического отклонения.

Рассмотрим пример, позволяющий почувствовать различие между средним квадратическим отклонением и средней ошибкой сред­него, а также уяснить, почему не следует пренебрегать средним квадратическим отклонением. Положим, исследователь, обследовав выбор­ку из 20 человек, пишет в статье, что средний сердечный выброс составлял 5,0 л/мин со средним квадратическим отклонением 1 л/мин. Мы знаем, что 95% нормально распределенной совокупности попа­дает в интервал среднее плюс-минус два средних квадратических отклонения. Тем самым, из статьи видно, что почти у всех обследован­ных сердечный индекс составил от 3 до 7 л/мин. Такие сведения весьма полезны, их легко использовать во врачебной практике. Увы, приведенный пример далек от реальности. Скорее автор укажет не среднее квадратическое отклонение, а среднюю ошибку сред­него. Тогда из статьи вы узнаете, что «сердечный выброс соста­вил (5,0 ± 0,22) л/мин». И если бы мы спутали среднюю ошиб­ку среднего со средним квадратическим отклонением, то пребывали бы в уверенности, что 95% совокупности заключено в интервал от 4,56 до 5,44 л/мин. На самом деле в этом интервале (с вероятно­стью 95%) находится среднее значение сердечного выброса. Впрочем, среднее квадратическое отклонение можно рассчитать са­мому – для этого нужно умножить среднюю ошибку средне­го на квадратный корень из объема выборки (численности груп­пы): 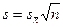. Правда, для этого нужно знать, что же именно приводит ав­тор – среднее квадратическое отклонение или среднюю ошибку средне­го.