Медиана и квартили.
Как выяснилось, для описания нормально распределённых признаков достаточно вычислить среднее и среднее квадратическое отклонение. Но для других распределений количественных признаков, например асимметричных, полагаться на среднее и среднее квадратическое отклонение нельзя.
Для описания таких данных лучше подходит не среднее, а медиана. Медиана – это значение, которое делит распределение пополам: половина значений больше медианы, половина – меньше (точнее, не больше). Для определения медианы надо все имеющиеся значения упорядочить по возрастанию или убыванию, в центре этого ряда и будет находиться медиана. Медиану обозначают Me.
Для характеристики разброса можно использовать квартили, они в отличие от медианы делит ряд не пополам, а на четыре части. Их будет три, четверть всех значений будет меньше первого квартиля, половина (две четверти) значений – меньше второго квартиля и три четверти значений – меньше третьего квартиля. Медиану получается можно считать вторым квартилем. Вычисляются квартили аналогично медиане, по упорядоченному ряду, только отслеживается четверть, две четверти и три четверти всех значений. Квартили обозначают соответственно Q1, Q2, Q3.
Конечно, медиана и квартили, в отличие от среднего и среднего квадратического отклонения, не дают полного описания распределения. Однако между первым и третьим квартилями находится половина значений – значит, мы можем судить, в каких пределах находится среднее значение. По положению медианы относительно 1-го и 3-го квартилей можно судить о том, насколько асимметрично распределение. И, наконец, теперь мы примерно знаем, какие значения показателя можно считать большими в данной совокупности (выше 3-го квартиля), а какие маленькими (ниже 1-го квартиля).
Для описания распределения чаще всего применяют 1-й и 3-й квартили. Однако ряд распределения можно разбить на любое другое число частей, а не только на две или четыре. Так разбиение на 10 частей будет осуществляться децилями, а на 100 частей процентилями. Порядок их вычисления аналогичен медиане и квартилям. Например, в качестве границ нормы лабораторных показателей часто используют 5-й и 95-й процентили.
Вычисление квартилей или процентилей, кроме того – хороший способ разобраться в том, насколько распределение близко к нормальному. Напомним, что для нормального распределения 95% значений заключено в пределах двух средних квадратических отклонений от среднего и 68% – в пределах одного среднего квадратического отклонения; медиана совпадает со средним. Соответствие между процентилями и числом средних квадратических отклонений от среднего таково:
| Процентили | 2,5 | 97,5 | |||
| Отклонения от среднего | m-2s | m-s | m | m+s | m+2s |
А соответствие между квартилями и отклонениями от среднего:
| Квартили | Q1 | Q2 | Q3 |
| Отклонения от среднего | m-0,7s | m | m+0,7s |
Если соответствие между квартилями или процентилями и отклонениями от среднего не слишком отличаются от приведенных, то распределение близко к нормальному и его можно описать при помощи среднего и среднего квадратического отклонения.
Есть еще одна, и очень важная, причина, по которой нужно знать, близко ли распределение к нормальному. Дело в том, что многие методы проверки гипотез, основаны на предположении, что распределение близко к нормальному. Только в этом случае эти методы будут надежны. Такие методы называются параметрические, т.е. основанные на параметрах распределения (нормального).
Выборочные оценки.
До сих пор нам удавалось получить данные обо всех объектах совокупности, поэтому мы могли точно рассчитать значения среднего, дисперсии и среднего квадратического отклонения. На самом деле обследовать все объекты совокупности удается редко: обычно довольствуются изучением выборки, полагая, что эта выборка отражает свойства совокупности. Выборку, отражающую свойства совокупности, называют представительной или репрезентативной. Основным способом обеспечения репрезентативности является случайный характер отбора элемента из совокупности в выборку. Имея дело с выборкой, мы, конечно, не узнаем точных значений среднего и среднего квадратического отклонения, но можем оценить их. Оценка среднего, вычисленная по выборке, называется выборочным средним. Выборочное среднее обозначают 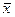 и вычисляют по формуле:
и вычисляют по формуле: 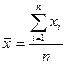 , где n – объем выборки.
, где n – объем выборки.
Оценка среднего квадратического отклонения называется выборочным средним квадратическим отклонением (s) и определяется следующим образом: 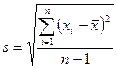 .
.
Эта формула отличается от формулы для среднего квадратического отклонения по совокупности. Во-первых, среднее m или 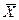 заменяется его выборочной оценкой –
заменяется его выборочной оценкой – 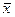 . Во-вторых, в знаменателе из числа членов выборки вычитается единица. Это определяется требованием несмещённости оценки относительно истинного значения. Можно дать и такое нестрогое объяснение: разброс значений в пределах выборки никогда не бывает столь большим, как во всей совокупности, и деление не на n, а на n-1 компенсирует возникающее занижение оценки среднего квадратического отклонения.
. Во-вторых, в знаменателе из числа членов выборки вычитается единица. Это определяется требованием несмещённости оценки относительно истинного значения. Можно дать и такое нестрогое объяснение: разброс значений в пределах выборки никогда не бывает столь большим, как во всей совокупности, и деление не на n, а на n-1 компенсирует возникающее занижение оценки среднего квадратического отклонения.
Дата добавления: 2016-02-04; просмотров: 6555;
