Критерий хи-квадрат.
Критерий хи-квадрат в отличие от критерия z применяется для сравнения любого количества групп.
Исходные данные: таблица сопряжённости.
Пример таблицы сопряженности минимальной размерности 2*2, приведен ниже. A,B,C,D – так называемые, реальные частоты.
| Признак 1 | Признак 2 | Всего | |
| Группа 1 | A | B | A+B |
| Группа 2 | C | D | C+D |
| Всего | A+C | B+D | A+B+C+D |
Расчёт критерия основан на сравнении реальных частот и ожидаемых частот, которые вычисляются в предположении отсутствия взаимного влияния сравниваемых признаков друг на друга. Таким образом, если реальные и ожидаемые частоты достаточно близки друг к другу, то влияния нет и значит признаки будут распределены примерно одинаково по группам.
Исходные данные для применения этого метода должны быть занесены в таблицу сопряженности, по столбцам и по строчкам которой указываются варианты значений изучаемых признаков. Числа в этой таблице будут называться реальными или экспериментальными частотами. Далее необходимо рассчитать ожидаемые частоты исходя из предположения, что сравниваемые группы абсолютно равны по распределению признаков. В этом случае пропорции по итоговой строчке или столбцу «всего» должны сохраняться в любой строчке и столбце. Исходя из этого, определяются ожидаемые частоты (см. пример).
Затем рассчитывают значение критерия как сумму по всем ячейкам таблицы сопряженности отношения квадрата разности между реальной частотой и ожидаемой частотой к ожидаемой частоте:
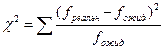 ,
,
где 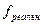 - реальная частота в ячейке;
- реальная частота в ячейке; 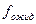 - ожидаемая частота в ячейке.
- ожидаемая частота в ячейке.
Для таблицы 2*2 можно рассчитать значение критерии без определения ожидаемых частот (с поправкой Йейтса на непрерывность):
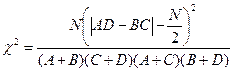 , где N = A+ B + C + D.
, где N = A+ B + C + D.
При расчёте по основной формуле для таблицы 2*2 (только для такой таблицы), также необходимо применить поправку Йейтса на непрерывность:
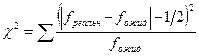 .
.
Критическое значение критерия 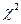 определяется по таблице (см. приложение) с учетом числа степеней свободы и уровня значимости. Уровень значимости принимают стандартным: 0,05; 0,01 или 0,001. Число степеней свободы определяется как произведение числа строк и столбцов таблицы сопряженности уменьшенных каждое на единицу:
определяется по таблице (см. приложение) с учетом числа степеней свободы и уровня значимости. Уровень значимости принимают стандартным: 0,05; 0,01 или 0,001. Число степеней свободы определяется как произведение числа строк и столбцов таблицы сопряженности уменьшенных каждое на единицу:
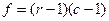 ,
,
где r – число строк (число градаций одного признака), с – число столбцов (число градаций другого признака). Это критическое значение можно определить в электронной таблице Microsoft Excel используя функцию =хи2обр(a, f), где вместо a надо ввести уровень значимости, а вместо f – число степеней свободы.
Если значение критерия хи-квадрат больше критического, то гипотезу о независимости признаков отвергают и их можно считать зависимыми на выбранном уровне значимости.
У этого метода есть ограничение по применимости: ожидаемые частоты должны быть 5 или более (для таблицы 2*2). Для произвольной таблицы это ограничение менее строгое: все ожидаемые частоты должны быть 1 или больше, а доля ячеек с ожидаемыми частотами меньше 5 не должна превышать 20%.
Из таблицы сопряженности большой размерности можно «вычленить» таблицы меньшей размерности и для них рассчитать значение критерия c2. Это фактически будут множественные сравнения, аналогичные описанным для критерия Стьюдента. В этом случае также надо применять поправку на множественные сравнения в зависимости от их количества.
Для проверки гипотезы с помощью критерия c2 в электронных таблицах Microsoft Excel можно применить следующую функцию:
= ХИ2ТЕСТ(фактический_интервал; ожидаемый_интервал).
Здесь фактический_интервал – исходная таблица сопряженности с реальными частотами (указываются только ячейки с самими частотами без заголовков и «всего»); ожидаемый_интервал – массив ожидаемых частот. Следовательно, ожидаемые частоты должны быть вычислены самостоятельно.
Пример:
В некотором городе произошла вспышка инфекционного заболевания. Есть предположение, что источником заражения явилась питьевая вода. Проверить это предположение решили с помощью выборочного опроса городского населения, по которому необходимо установить влияет ли количество выпиваемой воды на количество заболевших.
Исходные данные приведены в следующей таблице:
| Количество выпиваемой в среднем за день воды | Число заболевших | Число не заболевших | Всего |
| менее 1-го стакана | |||
| от 1-го до 4-х | |||
| 5 и более | |||
| Всего |
Рассчитаем ожидаемые частоты. Пропорция по всего должна сохраниться и внутри таблицы. Поэтому вычислим, например, какую долю составляют всего по строчкам в общей численности, получим для каждой строчки коэффициент. Такая же доля должна оказаться в каждой ячейке соответствующей строчки, поэтому для вычисления ожидаемой частоты в ячейке умножаем коэффициент на всего по соответствующему столбцу.
| Количество выпиваемой в среднем за день воды | Число заболевших | Число не заболевших | Всего | Коэффициент |
| менее 1-го стакана | 569*0,1463=83,2 | 525*0,1463=76,8 | 160/1094=0,1463 | |
| от 1-го до 4-х | 569*0,4781=272 | 525*0,4781=251 | 523/1094=0,4781 | |
| 5 и более | 569*0,3757=213,8 | 525*0,3757=197,2 | 411/1094=0,3757 | |
| Всего |
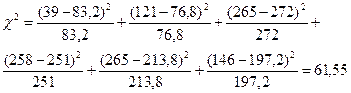
Число степеней свободы равно (3-1)*(2-1)=2. Критическое значение критерия 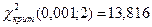 .
.
Экспериментальное значение больше критического (61,5>13,816), т.е. гипотеза об отсутствия влияния количества выпиваемой воды на заболеваемость отвергается с вероятностью ошибки менее 0,001. Таким образом, можно утверждать, что именно вода стала источником заболевания.
У обоих описанных критериев существуют ограничения, которые обычно не выполняются, если число наблюдений невелико или отдельные градации признаков редко встречаются. В этом случае используют точный критерий Фишера. Он основан на переборе всех возможных вариантов заполнения таблицы сопряженности при данной численности групп. Поэтому ручной расчет его довольно сложен. Для его расчёта можно воспользоваться статистическими пакетами прикладных программ.
ВЫВОДЫ.
Критерий z является аналогом критерия Стьюдента, но применяется для сравнения качественных признаков. Экспериментальное значение критерия рассчитывается как отношение разности долей к средней ошибке разности долей.
Критические значение критерия z равны соответствующим точкам нормированного нормального распределения: 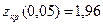 ,
, 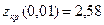 ,
, 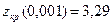 .
.
Критерий хи-квадрат применяется для сравнения любого количества групп по значениям качественных признаков. Исходные данные должны быть представлены в виде таблицы сопряжённости. Экспериментальное значение критерия рассчитывают как сумму по всем ячейкам таблицы сопряженности отношения квадрата разности между реальной частотой и ожидаемой частотой к ожидаемой частоте. Ожидаемые частоты вычисляются в предположении равенства сравниваемых признаков во всех группах. Критические значения определяются по таблицам распределения хи-квадрат.
ЛИТЕРАТУРА.
Гланц С. – Глава 5.
Реброва О.Ю. – Глава 10,11.
Лакин Г.Ф. – с. 120-123
Вопросы для самопроверки студентов.
1. В каких случаях можно применять критерий z?
2. На чём основано вычисление экспериментального значения критерия z?
3. Как найти критическое значение критерия z?
4. В каких случаях можно применять критерий c2 ?
5. На чём основано вычисление экспериментального значения критерия c2 ?
6. Как найти критическое значение критерия c2 ?
7. Что ещё можно применить для сравнения качественных признаков, если нельзя применить по ограничениям критерии z и c2 ?
Задачи.
№ 4, 5, 6, 14.
Дата добавления: 2016-02-04; просмотров: 4816;
