Численное дифференцирование
При решении многих практических задач возникает необходимость получить значения производных различных порядков функции f, заданной в виде таблицы или сложного аналитического выражения. В этих случаях применить непосредственно методы дифференцированного исчисления либо невозможно, либо затруднительно. Тогда используют приближенные методы численного дифференцирования.
Простейшие выражения для производных получаются в результате дифференцирования интерполяционных форм.
Итак, рассмотрим следующую задачу. На сетке 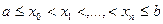 в узлах
в узлах 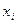 заданы значения
заданы значения 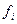 функции f, непрерывно дифференцируемой n+1+m раз. Требуется вычислить производную
функции f, непрерывно дифференцируемой n+1+m раз. Требуется вычислить производную 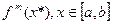 и оценить погрешность.
и оценить погрешность.
Один из возможных способов решения этой задачи заключается в следующем. Построим для функции f по узлам 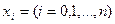 интерполяционный многочлен с остаточным членом
интерполяционный многочлен с остаточным членом 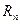 , так что
, так что
f (x)= 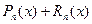 . (5.1)
. (5.1)
Продифференцируем правую и левую части соотношения (5.1) m раз и положим 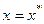 :
:
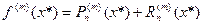 . (5.2)
. (5.2)
Для достаточно гладких функций, т.е. для функций с ограниченными производными, необходимым количеством узлов и заданной точностью величиной, величина 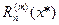 мала и
мала и 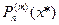 является хорошим приближенным для
является хорошим приближенным для 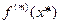 , так что можно положить
, так что можно положить
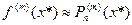 . (5.3)
. (5.3)
В практических расчетах численное дифференцирование оказывается весьма чувствительным к ошибкам в исходной информации, отбрасыванию членов ряда к другим подобным операциям. Кроме того, высокая точность интерполирования [малость 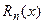 ] совсем не гарантирует высокой точности интерполяционной формулы для производной [малости
] совсем не гарантирует высокой точности интерполяционной формулы для производной [малости 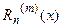 ]. Поэтому численное дифференцирование следует применять осторожно и, как правило, для небольших m.
]. Поэтому численное дифференцирование следует применять осторожно и, как правило, для небольших m.
Учитывая сказанное, а так же то, что вычисление высших производных может быть сведено к последовательному вычислению низших, остановимся более подробно на получении расчетных формул для 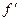 и
и 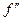 в узлах равномерной сетки. Для получения производных в узловых точках целесообразно использовать интерполяционный многочлен Стирлинга и его остаточный член. Так дифференцируя многочлен Стирлинга и его остаточный член по x и полагая
в узлах равномерной сетки. Для получения производных в узловых точках целесообразно использовать интерполяционный многочлен Стирлинга и его остаточный член. Так дифференцируя многочлен Стирлинга и его остаточный член по x и полагая 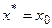 (
( 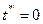 ), получим следующие выражения для производной:
), получим следующие выражения для производной:
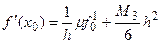 (k=1) (5.4)
(k=1) (5.4)
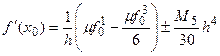 (k=2) (5.5)
(k=2) (5.5)
Дифференцируя многочлен Стирлинга два раза по x и вычисляя значение второй производной в точке 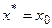 имеем
имеем
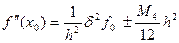 (k=1) (5.6)
(k=1) (5.6)
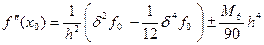 (k=2) (5.7)
(k=2) (5.7)
Для вычисления производной точно в середине между узлами 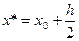 применяют многочлен Бесселя. В этом случае соответствующие формулы для производной имеют вид
применяют многочлен Бесселя. В этом случае соответствующие формулы для производной имеют вид
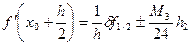 (k=1) (5.8)
(k=1) (5.8)
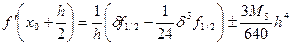 (k=2) (5.9)
(k=2) (5.9)
Практический интерес представляют также так называемые формулы одностороннего дифференцирования, позволяющие вычислить 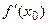 по узлам
по узлам 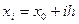 (i=0,1,…,k,… или i=0,- 1,…,- k,…). Построение этих формул удобно провести с помощью первого и второго интерполяционных многочленов Ньютона.
(i=0,1,…,k,… или i=0,- 1,…,- k,…). Построение этих формул удобно провести с помощью первого и второго интерполяционных многочленов Ньютона.
Дифференцируя первый многочлен Ньютона по x и вычисляя значение производной в точке 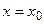 (t = 0) для k=1 и k=2 получим соответственно следующие формулы:
(t = 0) для k=1 и k=2 получим соответственно следующие формулы:
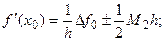 (5.10)
(5.10)
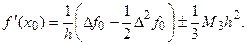 (5.11)
(5.11)
Аналогично, дифференцируя второй многочлен Ньютона, для k=-1 и k= - 2 соответственно имеем
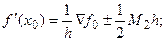 (5.12)
(5.12)
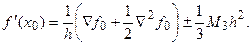 (5.13)
(5.13)
Приведем снова все формулы второго порядка, выразив входящие в них конечные разности непосредственно через значение функции 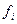 . Из соотношений (5.4), (5.6) и (5.8) имеем
. Из соотношений (5.4), (5.6) и (5.8) имеем
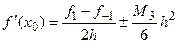 (5.14)
(5.14)
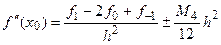 (5.15)
(5.15)
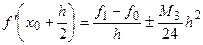 (5.16)
(5.16)
Соотношения (5.11) и (5.13) соответственно дают
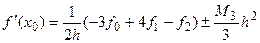 (5.17)
(5.17)
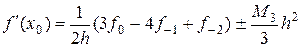 (5.18)
(5.18)
Из формул (5.17), (5.18) видно, что с уменьшением шага сетки уменьшается и погрешность метода. Однако если значения функции 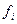 заданы приближенно, например, с одинаковой абсолютной погрешностью
заданы приближенно, например, с одинаковой абсолютной погрешностью 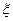 , то при использовании формул численного дифференцирования суммарная погрешность будет содержать дополнительное слагаемое, обратно пропорциональное
, то при использовании формул численного дифференцирования суммарная погрешность будет содержать дополнительное слагаемое, обратно пропорциональное 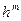 (m – порядок производной). Поэтому уменьшение h разумно лишь в определенных пределах.
(m – порядок производной). Поэтому уменьшение h разумно лишь в определенных пределах.
Иллюстрируя сказанное, рассмотрим правую часть формулы (5.16). Суммарная погрешность ее составляет
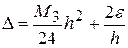 . (5.19)
. (5.19)
Приравнивая 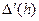 нулю, получаем точку экстремума функции
нулю, получаем точку экстремума функции 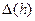 :
:
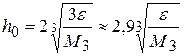 . (5.20)
. (5.20)
Так как 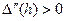 , то
, то 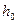 - точка минимума
- точка минимума 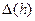 , причем:
, причем:
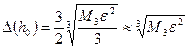 . (5.21)
. (5.21)
Аналогично, из формулы (5.15) для оптимального шага получаем выражение
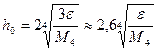 (5.22)
(5.22)
А из формулы (5.17) и (5.18) – выражение
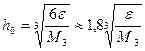 (5.23)
(5.23)
Таким образом, при вычислении производных предварительно следует определить оптимальный шаг исходной таблицы значений 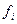 .
.
Пример 5.1. Вычислить 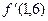 и
и 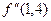 для функции
для функции 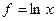 , заданной в виде таблицы (табл. 5.1), содержащей значение
, заданной в виде таблицы (табл. 5.1), содержащей значение 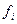 со всеми верными в широком смысле знаками. Оценить погрешность результата.
со всеми верными в широком смысле знаками. Оценить погрешность результата.
Таблица 5.1. Данные к примеру 5.1
| x | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 |
| f | 0,1823 | 0,2626 | 0,3364 | 0,4054 | 0,4700 |
Для вычисления требуемых производных применим соответственно формулы (5.18) и (5.15). Тогда, используя равенства (5.21) и (5.22), а также исходные данные, получим следующие значения для оптимального шага:
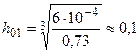 при вычислении
при вычислении 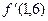 ;
;
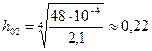 при вычислении
при вычислении 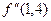 .
.
Так как табличные данные не позволяют выбрать в качестве шага 0,22, то за 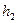 Принимаем ближайшее возможное число 0,2. Следовательно,
Принимаем ближайшее возможное число 0,2. Следовательно,
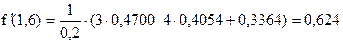 ,
,
причем суммарная погрешность не превышает
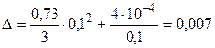 ;
;
и
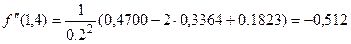 ,
,
причем суммарная погрешность не превышает
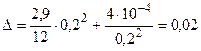 .
.
В некоторых случаях для определения производной задается только таблица значений функции. Тогда оценить погрешность невозможно. Приближенные значения производной вычисляются непосредственно по одной из формул (5.17) – (5.23) без учета погрешности.
Пример 5.2. Вычислить 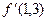 ,
, 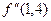 для функции f(x), заданной в виде таблицы (табл. 5).
для функции f(x), заданной в виде таблицы (табл. 5).
Таблица 5. Данные к примеру 5.2
| x | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 |
| y=f(x) | 0,18 | 0,26 | 0,34 | 0,41 | 0,47 |
На основании формул (5.17) и (5.19) получаем:
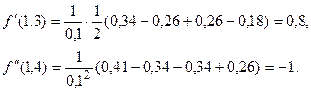
Дата добавления: 2015-11-06; просмотров: 1589;
